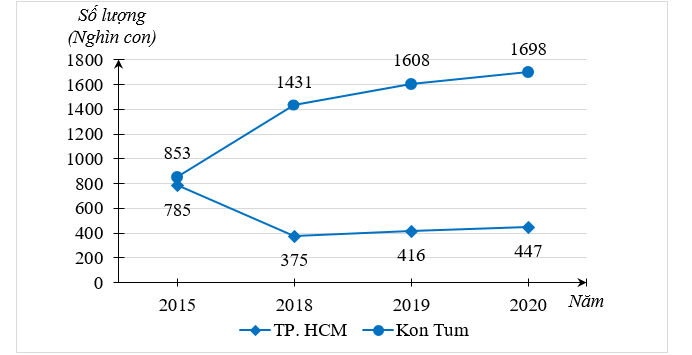
Biểu đồ đoạn thẳng ở hình bên dưới thống kê số lượng gia cầm ở TP. HCM và Kon Tum qua các năm 2015, 2018, 2019, 2020. (Nguồn: Niêm giám thống kê năm 2021).
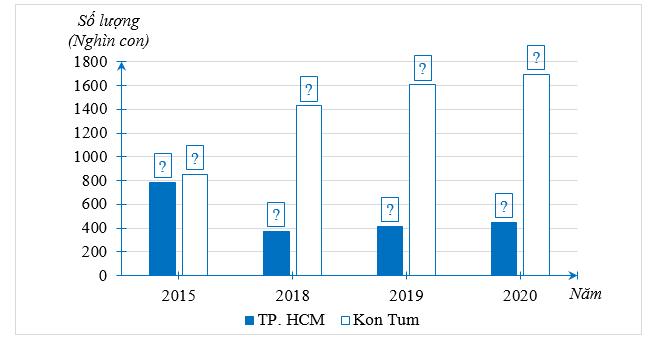
a) Hãy hoàn thành biểu đồ cột kép ở hình bên dưới để nhận được biểu đồ biểu diễn dữ liệu trong biểu đồ đoạn thẳng ở hình trên.
b) TP. HCM và Kon Tum trong năm 2020 lượng gia cầm ở đâu nhiều nhất? Nhiều nhất là bao nhiêu nghìn con?
c) Một bài báo đã nêu ra nhận định “Tổng số lượng gia cầm ở Kon Tum trong năm \[2015,\]\[2018,{\rm{ }}2019,{\rm{ }}2020\] là \[2023\] nghìn con và so với năm \[2018\] số lượng gia cầm ở TP. HCM tăng \(80\% \) so với số lượng gia cầm ở Kon Tum”. Em hãy cho biết nhận định trên bài báo có chính xác không?
d) Em hãy đề xuất một vài giải pháp để tăng số lượng gia cầm ở Kon Tum trong những năm tới để đạt hiệu quả trong chăn nuôi.
Biểu đồ đoạn thẳng ở hình bên dưới thống kê số lượng gia cầm ở TP. HCM và Kon Tum qua các năm 2015, 2018, 2019, 2020. (Nguồn: Niêm giám thống kê năm 2021).
a) Hãy hoàn thành biểu đồ cột kép ở hình bên dưới để nhận được biểu đồ biểu diễn dữ liệu trong biểu đồ đoạn thẳng ở hình trên.
b) TP. HCM và Kon Tum trong năm 2020 lượng gia cầm ở đâu nhiều nhất? Nhiều nhất là bao nhiêu nghìn con?
c) Một bài báo đã nêu ra nhận định “Tổng số lượng gia cầm ở Kon Tum trong năm \[2015,\]\[2018,{\rm{ }}2019,{\rm{ }}2020\] là \[2023\] nghìn con và so với năm \[2018\] số lượng gia cầm ở TP. HCM tăng \(80\% \) so với số lượng gia cầm ở Kon Tum”. Em hãy cho biết nhận định trên bài báo có chính xác không?
d) Em hãy đề xuất một vài giải pháp để tăng số lượng gia cầm ở Kon Tum trong những năm tới để đạt hiệu quả trong chăn nuôi.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) Ta hoàn thành được biểu đồ cột kép biểu diễn dữ liệu trong biểu đồ đoạn thẳng như sau:
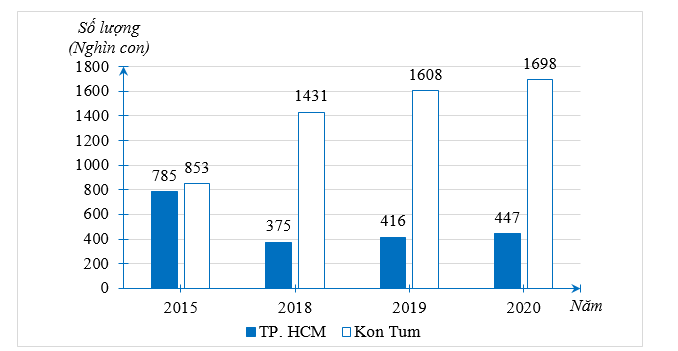
b) Trong năm 2020 lượng gia cầm ở Kon Tum nhiều nhất, là 1698 nghìn con.
c) Tổng số lượng gia cầm ở Kon Tum trong năm \[2015,\]\[2018,{\rm{ }}2019,{\rm{ }}2020\] là:
\(853 + 1\,\,431 + 1\,\,608 + 1\,\,698 = 5\,\,590\) (nghìn con).
Trong năm 2018, số lượng gia cầm ở TP. HCM \[(375\] nghìn con) ít hơn so với số lượng gia cầm ở Kon Tum \[(1{\rm{ }}431\] nghìn con) nên nhận định trên bài báo không chính xác.
d) Một vài giải pháp để tăng số lượng gia cầm ở Kon Tum trong những năm tới để đạt hiệu quả trong chăn nuôi:
⦁ Đẩy mạnh tuyên truyền, vận động nhân dân chăm sóc tốt đàn gia cầm hiện có;
⦁ Mạnh dạn đầu tư phát triển quy mô chăn nuôi, đa dạng các loại gia cầm;
⦁ Chú trọng việc lai tạo và cải thiện giống gia cầm địa phương;
⦁ Thường xuyên thực hiện vệ sinh tiêu độc khử trùng; …
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
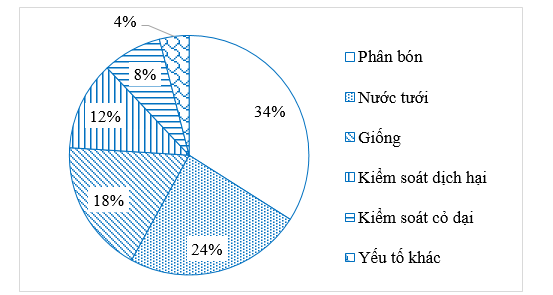
a) Yếu tố Phân bón (chiếm \(34\% )\) ảnh hưởng đến sinh trưởng của cây trồng nhiều nhất.
b) Trong các yếu tố ảnh hưởng đến sinh trưởng của cây thì Yếu tố kiểm soát dịch hại gấp số lần Yếu tố khác là: \(\frac{{12\% }}{{4\% }} = 3\) (lần).
c) Một vài biện pháp khắc phục tình trạng vấn đề tưới nước để làm giảm thiệt hại trong việc trồng trọt: khoan thêm giếng, lắp đặt thêm ống dẫn nước từ các hồ chứa, xây dựng phương án tưới cho phù hợp với từng loại cây trồng, áp dụng phương pháp tưới tiết kiệm nước theo hình thức khô – nước xen kẽ, chỉ vô nước giai đoạn bón phân.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
a) Ta lập bảng số liệu thống kê số giờ nắng của các tháng trong năm 2022 như sau:
|
Tháng |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Tổng số giờ nắng (h) |
\[34,4\] |
\[27,5\] |
\[49,4\] |
\[108,2\] |
\[88,8\] |
\[186,6\] |
\[190,7\] |
\[151,7\] |
\[133,2\] |
\[165,0\] |
\[126,2\] |
\[102,1\] |
b) Ta hoàn thành được biểu đồ đoạn thẳng biểu diễn số giờ nắng của các tháng trong năm 2022 tại trạm quan trắc Nam Định như sau:
c) Số giờ nắng tại Nam Định trong tháng 7 là cao nhất \(\left( {190,7\,\,\,h} \right)\) và tháng 2 là thấp nhất \(\left( {27,5\,\,h} \right).\)
d) Số giờ nắng của các tháng trong năm 2022 tại Nam Định giảm trong các khoảng thời gian: tháng 1 – tháng 2; tháng 4 – tháng 5; tháng 7 – tháng 8; tháng 8 – tháng 9; tháng 10 – tháng 11; tháng 11 – tháng 12.
Số giờ nắng của các tháng trong năm 2022 tại Nam Định tăng trong các khoảng thời gian: tháng 2 – tháng 3; tháng 3 – tháng 4; tháng 5 – tháng 6; tháng 6 – tháng 7; tháng 9 – tháng 10.
e) So với tháng 9, số giờ nắng tại Nam Định trong tháng 10 bằng \(\frac{{165}}{{133,2}} \cdot 100\% \approx 123,87\% .\)
Khi đó tháng 10 tăng khoảng \(123,87\% - 100\% = 23,87\% \) so với tháng 9.
Vậy thông tin của bài báo đó không chính xác.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Hình dưới đây thể hiện số lượng học sinh tham gia đăng kí hai Câu lạc bộ cầu lông và cờ vua của trường:
a) Lập bảng thống kê cho biểu đồ trên.
b) Cho biết sự khác nhau về việc tham gia đăng kí hai Câu lạc bộ cầu lông và cờ vua của hai lớp 8A3 và 8A4.
c) Nếu lớp 8A1 có số lượng học sinh tham gia Câu lạc bộ cầu lông chiếm \(25\% \) tổng số học sinh cả lớp. Hãy tính xem lớp 8A1 có bao nhiêu học sinh.
d) Hãy so sánh tổng số học sinh tham gia Câu lạc bộ cầu lông và Câu lạc bộ cờ vua.
Hình dưới đây thể hiện số lượng học sinh tham gia đăng kí hai Câu lạc bộ cầu lông và cờ vua của trường:
a) Lập bảng thống kê cho biểu đồ trên.
b) Cho biết sự khác nhau về việc tham gia đăng kí hai Câu lạc bộ cầu lông và cờ vua của hai lớp 8A3 và 8A4.
c) Nếu lớp 8A1 có số lượng học sinh tham gia Câu lạc bộ cầu lông chiếm \(25\% \) tổng số học sinh cả lớp. Hãy tính xem lớp 8A1 có bao nhiêu học sinh.
d) Hãy so sánh tổng số học sinh tham gia Câu lạc bộ cầu lông và Câu lạc bộ cờ vua.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập