Đỉnh Fansipan (Lào Cai) cao \(3143{\rm{ m,}}\) là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi, người ta đặt một chóp làm bằng inox có dạng hình chóp tam giác đều dài \(60{\rm{ cm,}}\)chiều cao \(90{\rm{ cm}}\) (như hình vẽ).
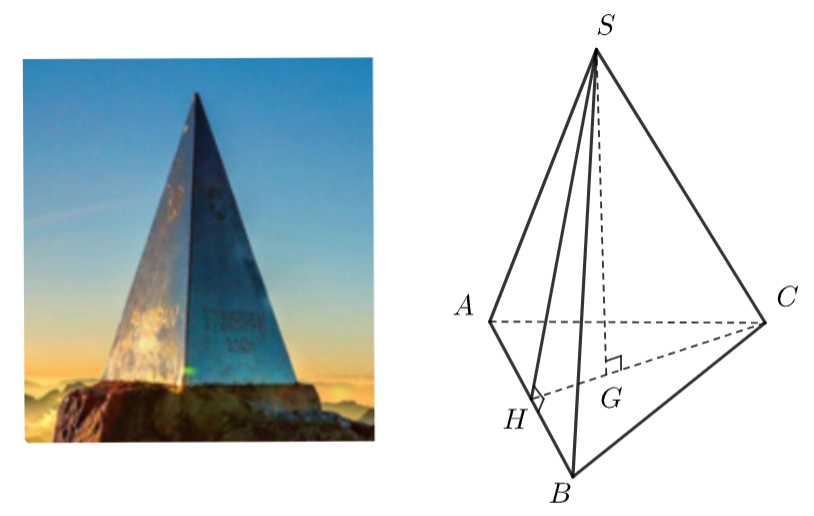
a) Tam giác đều \(ABC\) có \(CH\) là đường trung tuyến.
b) Độ dài đường trung tuyến \(CH\) bằng \(30\sqrt 3 {\rm{ cm}}\).
c) Độ dài cạnh \(SH\) nhỏ hơn độ dài cạnh \(CH\).
d) Diện tích xung quanh của hình chóp là \(8635{\rm{ c}}{{\rm{m}}^{\rm{2}}}.\)
Đỉnh Fansipan (Lào Cai) cao \(3143{\rm{ m,}}\) là đỉnh núi cao nhất Đông Dương. Trên đỉnh núi, người ta đặt một chóp làm bằng inox có dạng hình chóp tam giác đều dài \(60{\rm{ cm,}}\)chiều cao \(90{\rm{ cm}}\) (như hình vẽ).
a) Tam giác đều \(ABC\) có \(CH\) là đường trung tuyến.
b) Độ dài đường trung tuyến \(CH\) bằng \(30\sqrt 3 {\rm{ cm}}\).
c) Độ dài cạnh \(SH\) nhỏ hơn độ dài cạnh \(CH\).
d) Diện tích xung quanh của hình chóp là \(8635{\rm{ c}}{{\rm{m}}^{\rm{2}}}.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: a) Đ. b) Đ. c) S. d) S.
⦁ Mặt đáy của hình chóp \(S.ABC\) là một tam giác đều \(ABC\) có cạnh \(60{\rm{ cm}}{\rm{.}}\)
Gọi đường cao của mặt đáy là \(CH\) nên \(CH\) đồng thời là đường trung tuyến của tam giác đều \(ABC.\)
Do đó ý a) đúng.
⦁ Vì \(HA = HB = \frac{{AB}}{2} = 30{\rm{ cm}}{\rm{.}}\)
Áp dụng định lý Pythagore vào \(\Delta BHC\) vuông tại \(H\), ta có:
\(C{B^2} = H{B^2} + H{C^2}\) hay \({60^2} = {30^2} + H{C^2}\)
Suy ra \(C{H^2} = {60^2} - {30^2} = 2{\rm{ }}700\) nên \(CH = \sqrt {2700} = 30\sqrt 3 {\rm{ }}\left( {{\rm{cm}}} \right)\). (1)
Gọi \(G\) là trọng tâm của mặt đáy nên \(GH = \frac{1}{3}HC = \frac{{30\sqrt 3 }}{3} = 10\sqrt 3 {\rm{ }}\left( {{\rm{cm}}} \right)\).
Hình chóp \(S.ABC\) có đường cao \(SG\) nên \(SG \bot HC.\)
Áp dụng định lý Pythagore vào \[\Delta SHG\] vuông tại \(G\), ta có:
\(S{H^2} = S{G^2} + H{G^2}\)\( = {90^2} + {30^2} = 9000\)
Suy ra \(SH = \sqrt {9000} = 30\sqrt {10} {\rm{ cm}}{\rm{.}}\) (2)
Từ (1) và (2) suy ra độ dài cạnh \(SH\) lớn hơn độ dài cạnh \(CH\). Do đó ý c) sai.
⦁ Nửa chu vi đáy là: \(P = \frac{1}{2}\left( {60 + 60 + 60} \right) = 90{\rm{ }}\left( {{\rm{cm}}} \right)\)
Vậy diện tích xung quanh của hình chóp là \(S = P.d = 90.30\sqrt {10} \approx 8538{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\). Do đó ý d) sai.
Vậy: a) Đ. b) Đ. c) S. d) S.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp số: 2.
Ta có \(\frac{{x + 1}}{{x - 2}} + \frac{{x - 2}}{{x + 2}} + \frac{{x - 14}}{{{x^2} - 4}}\)
\[ = \frac{{\left( {x + 1} \right)\left( {x + 2} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} + \frac{{{{\left( {x - 2} \right)}^2}}}{{x + 2}} + \frac{{x - 14}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\]
\[ = \frac{{\left( {x + 1} \right)\left( {x + 2} \right) + {{\left( {x - 2} \right)}^2} + x - 14}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\]
\[ = \frac{{{x^2} + 3x + 2 + {x^2} - 4x + 4 + x - 14}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}\]
\[ = \frac{{2{x^2} - 8}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} = \frac{{2\left( {x - 2} \right)\left( {x + 2} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} = 2.\]
![Cho hình vẽ, biết \[\widehat B + \widehat D = 135^\circ \,,\,\,\widehat {BAD} = \frac{{7x}}{2}\]. Tính số đo góc \[\widehat {{C_1}}\] (đơn vị: độ). (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/29-1758432859.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Đáp số: 30.
Xét tứ giác \(ABCD\) có \(\widehat {BAD} + \widehat B + \widehat {BCD} + \widehat D = 360^\circ \).
Suy ra \(\frac{{7x}}{2} + 4x + 135^\circ = 360^\circ \) hay \(\frac{{15x}}{2} = 225^\circ \) nên \(x = 30^\circ .\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Bộ nam châm xếp hình có dạng hình chóp tam giác đều (như hình ảnh) có độ dài cạnh đáy khoảng 6 cm và mặt bên có đường cao khoảng 7 cm. Tính diện tích xung quanh bộ nam châm xếp hình đó theo đơn vị \[{\rm{c}}{{\rm{m}}^{\rm{2}}}\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/24-1758432821.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập