Bình đọc một cuốn sách trong 4 ngày. Ngày thứ nhất đọc được \(\frac{1}{5}\) cuốn sách, ngày thứ hai đọc được \(\frac{1}{3}\) cuốn sách, ngày thứ ba đọc được \(\frac{1}{4}\) cuốn sách.
a) Ba ngày đầu Bình đọc được \(\frac{{47}}{{60}}\) cuốn sách.
b) Ngày thứ tư Bình đọc được \(\frac{{13}}{{60}}\) cuốn sách.
c) Ngày thứ tư bạn Bình đọc được nhiều nhất trong bốn ngày.
d) Hai ngày đầu bạn Bình đọc được nhiều hơn hai ngày sau.
Bình đọc một cuốn sách trong 4 ngày. Ngày thứ nhất đọc được \(\frac{1}{5}\) cuốn sách, ngày thứ hai đọc được \(\frac{1}{3}\) cuốn sách, ngày thứ ba đọc được \(\frac{1}{4}\) cuốn sách.
a) Ba ngày đầu Bình đọc được \(\frac{{47}}{{60}}\) cuốn sách.
b) Ngày thứ tư Bình đọc được \(\frac{{13}}{{60}}\) cuốn sách.
c) Ngày thứ tư bạn Bình đọc được nhiều nhất trong bốn ngày.
d) Hai ngày đầu bạn Bình đọc được nhiều hơn hai ngày sau.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là:a) Đúng b) Đúng c) Sai d) Đúng
• Ba ngày đầu Bình đọc được số phần cuốn sách là: \(\frac{1}{5} + \frac{1}{3} + \frac{1}{4} = \frac{{47}}{{60}}\) (cuốn sách). Do đó, ý a) là đúng.
• Ngày thứ tư, bình đọc được số phần cuốn sách là: \(1 - \frac{{47}}{{60}} = \frac{{13}}{{60}}\) (cuốn sách). Do đó, ý b) là đúng.
• Nhận thấy \(\frac{1}{5} = \frac{{12}}{{60}};{\rm{ }}\frac{1}{3} = \frac{{20}}{{60}};{\rm{ }}\frac{1}{4} = \frac{{15}}{{60}}\). Do đó, \(\frac{{12}}{{60}} < \frac{{13}}{{60}} < \frac{{15}}{{60}} < \frac{{20}}{{60}}\) hay \(\frac{1}{5} < \frac{{13}}{{60}} < \frac{1}{4} < \frac{1}{3}\).
Vậy ngày thứ hai bạn Bình đọc được nhiều sách nhất. Do đó, ý c) là sai.
• Hai ngày đầu bạn Bình đọc được số phần cuốn sách là: \(\frac{1}{5} + \frac{1}{3} = \frac{8}{{15}}\) (cuốn sách)
Hai ngày sau bạn Bình đọc được số phần cuốn sách là: \(\frac{1}{4} + \frac{{13}}{{60}} = \frac{7}{{15}}\) (cuốn sách)
Do đó, hai ngày đầu bạn Bình đọc được nhiều hơn hai ngày sau.
Do đó, ý d) là đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: a) Sai b) Đúng c) Sai d) Đúng
Ta có:
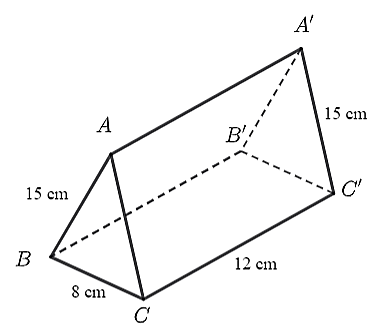
• Mặt đáy của hình lăng trụ \(ABC.A'B'C'\) là tam giác \(ABC\) và tam giác \(A'B'C'\). Do đó, ý a) là sai.
• Có \(AC = A'C' = 15{\rm{ cm}}{\rm{.}}\) Do đó, ý b) là đúng.
• Chu vi đáy của lăng trụ là: \(15 + 15 + 8 = 38\) (cm). Do đó, ý c) là sai.
• Diện tích xung quanh của hình lăng trụ \(ABC.A'B'C'\) là: \(38 \cdot 12 = 456{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\). Do đó, ý d) là đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án: 3
Ta có: \(\frac{{x + 4}}{{30}}\) có mẫu số \(30 = 2 \cdot 5 \cdot 3\). Do đó, để viết được phân số dưới dạng số thập phân hữu hạn thì tử số \(\left( {x + 4} \right)\) là số chia hết cho \(3\).
Có \(x \in \mathbb{N},x < 10\) nên \(0 \le x < 10\) Do đó, \(0 + 4 \le x + 4 < 10 + 4\) hay \(4 \le x + 4 < 14\).
Suy ra \(x + 4 \in \left\{ {6;9;12} \right\}\) nên \(x \in \left\{ {2;5;8} \right\}\).
Vậy có 3 số tự nhiên \(x < 10\) thỏa mãn yêu cầu bài toán.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập