Một căn phòng có dạng hình hộp chữ nhật với chiều dài là 6 m; chiều rộng 4,5 m và chiều cao 4 m. Chủ nhà dự định ốp gỗ mặt nền và một phần tường với độ cao gỗ ốp lên tường là 1,5 m. Chi phí mỗi mét vuông là 600 000 đồng (kể cả công và gỗ ốp). Hỏi để ốp gỗ căn phòng như dự định, chủ nhà cần thanh toán bao nhiêu tiền?
Một căn phòng có dạng hình hộp chữ nhật với chiều dài là 6 m; chiều rộng 4,5 m và chiều cao 4 m. Chủ nhà dự định ốp gỗ mặt nền và một phần tường với độ cao gỗ ốp lên tường là 1,5 m. Chi phí mỗi mét vuông là 600 000 đồng (kể cả công và gỗ ốp). Hỏi để ốp gỗ căn phòng như dự định, chủ nhà cần thanh toán bao nhiêu tiền?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Diện tích nền căn phòng là: \({S_d} = 6\,\,.\,\,4,5 = 27\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\)
Chu vi đáy của hình hộp chữ nhật là:
\({C_d} = 2\,\,.\,\,\left( {6 + 4,5} \right) = 21\,\,\left( {\rm{m}} \right)\)
Diện tích tường phòng ốp là:
\[{S_{xq}} = 21\,\,.\,\,1,5 = 31,5\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\]
Tổng diện tích cần ốp gỗ là:
\(S = {S_d} + {S_{xq}} = 27 + 31,5 = 58,5\,\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\)
Số tiền phải chi cho ốp gỗ căn phòng là:
\(58,5\,\,.\,\,600{\rm{ 000 = 35 100 000}}\) (đồng)
Vậy chủ nhà cần thanh toán 35 100 000 đồng để ốp căn phòng theo dự định.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
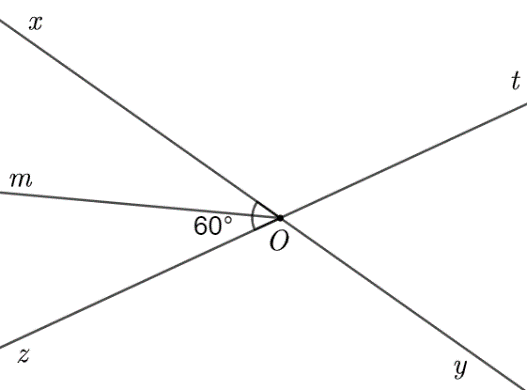
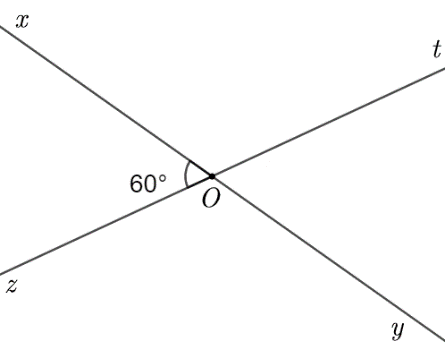
a) Các cặp góc đối đỉnh trong hình là: \(\widehat {xOz}\) và \(\widehat {tOy}\); \(\widehat {xOt}\) và \(\widehat {tOy}\).
b) Từ hình vẽ ta thấy \(\widehat {xOz} = 60^\circ \)
Vì \(\widehat {xOz}\) và \(\widehat {tOy}\) là hai góc đối đỉnh nên \(\widehat {xOz} = \widehat {tOy} = 60^\circ \).
Vì góc \(\widehat {xOz}\)và \(\widehat {xOt}\) là hai góc kề bù nên \(\widehat {xOz} + \widehat {xOt} = 180^\circ \).Suy ra \(\widehat {xOt} = 180^\circ - \widehat {xOz} = 180^\circ - 60^\circ = 120^\circ \).
Do đó \(\widehat {xOt} = 120^\circ \).
Vì \(Om\) là tia phân giác của \(\widehat {xOz}\) nên \(\widehat {mOx} = \widehat {mOz} = \frac{{\widehat {xOz}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \).
Vậy \(\widehat {tOy} = 60^\circ ;\,\,\widehat {xOt} = 120^\circ ;\,\,\widehat {mOx} = 30^\circ \).
Lời giải
a) Học sinh vẽ hình đúng số đo góc.
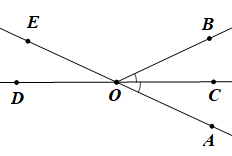
Các góc kề bù với góc \(AOC\) là \(\widehat {AOD},\widehat {COE}\).
b) Ta có: \(\widehat {AOB} + \widehat {BOE} = 180^\circ \) (hai góc kề bù)Suy ra \(\widehat {BOE} = 180^\circ - \widehat {AOB} = 180^\circ - 50^\circ = 130^\circ \).
Vì tia \(OC\) là tia phân giác của góc \(AOB\) nên \(\widehat {AOC} = \frac{1}{2}\widehat {AOB} = 25^\circ \).
Ta có \(\widehat {AOC} + \widehat {AOD} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {AOD} = 180^\circ - \widehat {AOC} = 180^\circ - 25^\circ = 155^\circ \).
Vậy \(\widehat {BOE} = 130^\circ \,;\,\,\widehat {AOD} = 155^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập