Tìm \(n \in \mathbb{Z}\) để các số hữu tỉ sau là những số nguyên:
g) \(\frac{{4n - 1}}{{3 - 2n}}\).
g) \(\frac{{4n - 1}}{{3 - 2n}}\).
Quảng cáo
Trả lời:
g) Ta có \(\frac{{4n - 1}}{{3 - 2n}} = \frac{{2\left( {2n - 3} \right) + 5}}{{ - \left( {2n - 3} \right)}} = - 2 - \frac{5}{{2n - 3}}\).
Để \(\frac{{4n - 1}}{{3 - 2n}}\) là số nguyên thì \[5\,\, \vdots \,\,\left( {2n - 3} \right)\] nên \[2n - 3 \in \left\{ { \pm 1\,;\, \pm 5} \right\}\].
Ta có bảng giá trị sau:
|
\[2n - 3\] |
\[ - 1\] |
1 |
\[ - 5\] |
5 |
|
\[2n\] |
2 |
4 |
\[ - 2\] |
8 |
|
\[n\] |
1 |
2 |
\[ - 1\] |
4 |
Vậy \(n \in \left\{ { \pm 1\,;\,\,2\,;\,\,4} \right\}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
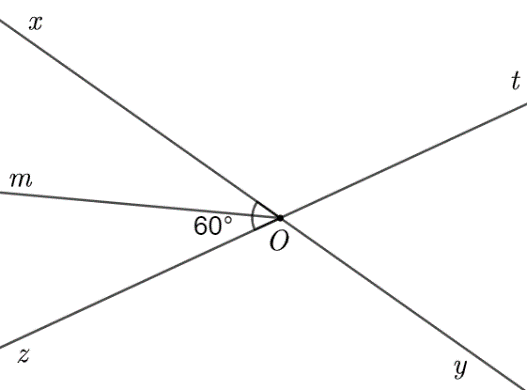
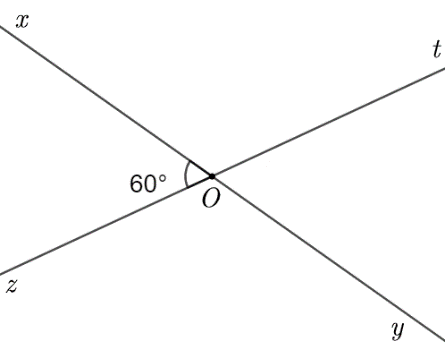
a) Các cặp góc đối đỉnh trong hình là: \(\widehat {xOz}\) và \(\widehat {tOy}\); \(\widehat {xOt}\) và \(\widehat {tOy}\).
b) Từ hình vẽ ta thấy \(\widehat {xOz} = 60^\circ \)
Vì \(\widehat {xOz}\) và \(\widehat {tOy}\) là hai góc đối đỉnh nên \(\widehat {xOz} = \widehat {tOy} = 60^\circ \).
Vì góc \(\widehat {xOz}\)và \(\widehat {xOt}\) là hai góc kề bù nên \(\widehat {xOz} + \widehat {xOt} = 180^\circ \).Suy ra \(\widehat {xOt} = 180^\circ - \widehat {xOz} = 180^\circ - 60^\circ = 120^\circ \).
Do đó \(\widehat {xOt} = 120^\circ \).
Vì \(Om\) là tia phân giác của \(\widehat {xOz}\) nên \(\widehat {mOx} = \widehat {mOz} = \frac{{\widehat {xOz}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \).
Vậy \(\widehat {tOy} = 60^\circ ;\,\,\widehat {xOt} = 120^\circ ;\,\,\widehat {mOx} = 30^\circ \).
Lời giải
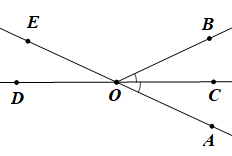
a) Học sinh vẽ hình đúng số đo góc.
Các góc kề bù với góc \(AOC\) là \(\widehat {AOD},\widehat {COE}\).
b) Ta có: \(\widehat {AOB} + \widehat {BOE} = 180^\circ \) (hai góc kề bù)Suy ra \(\widehat {BOE} = 180^\circ - \widehat {AOB} = 180^\circ - 50^\circ = 130^\circ \).
Vì tia \(OC\) là tia phân giác của góc \(AOB\) nên \(\widehat {AOC} = \frac{1}{2}\widehat {AOB} = 25^\circ \).
Ta có \(\widehat {AOC} + \widehat {AOD} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {AOD} = 180^\circ - \widehat {AOC} = 180^\circ - 25^\circ = 155^\circ \).
Vậy \(\widehat {BOE} = 130^\circ \,;\,\,\widehat {AOD} = 155^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.