Một cửa hàng nhập một lô gồm 100 máy tính Casio với giá nhập là \(480{\rm{ 000}}\) đồng một sản phẩm. Sau đó khi bán 70 chiếc với tiền lãi bằng \(30\% \) giá nhập, cửa hàng bán số máy còn lại với giá bằng \(70\% \) giá bán trước đó. Hỏi sau khi bán hết lô hàng thì cửa hành lãi hay lỗ bao nhiêu tiền?
Một cửa hàng nhập một lô gồm 100 máy tính Casio với giá nhập là \(480{\rm{ 000}}\) đồng một sản phẩm. Sau đó khi bán 70 chiếc với tiền lãi bằng \(30\% \) giá nhập, cửa hàng bán số máy còn lại với giá bằng \(70\% \) giá bán trước đó. Hỏi sau khi bán hết lô hàng thì cửa hành lãi hay lỗ bao nhiêu tiền?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Cửa hàng đã bán 70 chiếc máy tính với tiền lãi bằng 30% giá vốn. Tức là giá bán mỗi chiếc máy tính bằng \(100\% + 30\% = 130\% \) so với giá vốn.
Khi đó, giá tiền bán 70 chiếc máy tính này là:
\(70 \cdot 480{\rm{ 000}} \cdot 130\% = 560 \cdot 130\% = 43{\rm{ }}680{\rm{ }}000\) (đồng).
Cửa hàng đã bán số máy còn lại với mức giá bằng 70% giá bán trước đó. Tức là bán 30 chiếc máy tính còn lại, giá bán mỗi chiếc bằng \(130\% \cdot 70\% = 91\% \) so với giá mua.
Khi đó, giá tiền bán 30 chiếc máy tính này là:
\(30 \cdot 480{\rm{ }}000 \cdot 91\% = 13{\rm{ }}104{\rm{ }}000\) (đồng)
Số tiền thu được khi bán hết 100 chiếc máy tính là: \(43{\rm{ }}680{\rm{ }}000 + 13{\rm{ }}104{\rm{ }}000 = 56{\rm{ }}784{\rm{ }}000\) (đồng).
Số tiền bỏ ra khi mua 100 chiếc máy tính là: \(100 \cdot 480{\rm{ 000}} = 48{\rm{ }}000{\rm{ }}000\) (đồng)
Vì \(56{\rm{ }}784{\rm{ 00}}0 > {\rm{48 000 000}}\) nên cửa hàng đã lãi.
Số tiền lãi cửa hàng thu về là: \(56{\rm{ }}784{\rm{ 00}}0 - {\rm{48 000 000}} = 8{\rm{ 784 000}}\) (đồng).
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
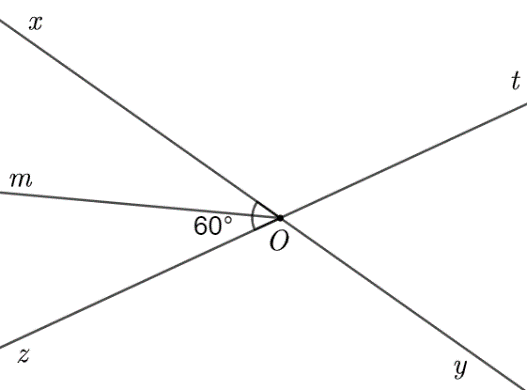
a) Các cặp góc đối đỉnh trong hình là: \(\widehat {xOz}\) và \(\widehat {tOy}\); \(\widehat {xOt}\) và \(\widehat {tOy}\).
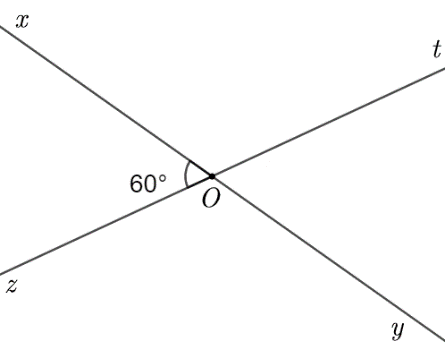
b) Từ hình vẽ ta thấy \(\widehat {xOz} = 60^\circ \)
Vì \(\widehat {xOz}\) và \(\widehat {tOy}\) là hai góc đối đỉnh nên \(\widehat {xOz} = \widehat {tOy} = 60^\circ \).
Vì góc \(\widehat {xOz}\)và \(\widehat {xOt}\) là hai góc kề bù nên \(\widehat {xOz} + \widehat {xOt} = 180^\circ \).Suy ra \(\widehat {xOt} = 180^\circ - \widehat {xOz} = 180^\circ - 60^\circ = 120^\circ \).
Do đó \(\widehat {xOt} = 120^\circ \).
Vì \(Om\) là tia phân giác của \(\widehat {xOz}\) nên \(\widehat {mOx} = \widehat {mOz} = \frac{{\widehat {xOz}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \).
Vậy \(\widehat {tOy} = 60^\circ ;\,\,\widehat {xOt} = 120^\circ ;\,\,\widehat {mOx} = 30^\circ \).
Lời giải
a) Học sinh vẽ hình đúng số đo góc.
Các góc kề bù với góc \(AOC\) là \(\widehat {AOD},\widehat {COE}\).
b) Ta có: \(\widehat {AOB} + \widehat {BOE} = 180^\circ \) (hai góc kề bù)Suy ra \(\widehat {BOE} = 180^\circ - \widehat {AOB} = 180^\circ - 50^\circ = 130^\circ \).
Vì tia \(OC\) là tia phân giác của góc \(AOB\) nên \(\widehat {AOC} = \frac{1}{2}\widehat {AOB} = 25^\circ \).
Ta có \(\widehat {AOC} + \widehat {AOD} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {AOD} = 180^\circ - \widehat {AOC} = 180^\circ - 25^\circ = 155^\circ \).
Vậy \(\widehat {BOE} = 130^\circ \,;\,\,\widehat {AOD} = 155^\circ .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo