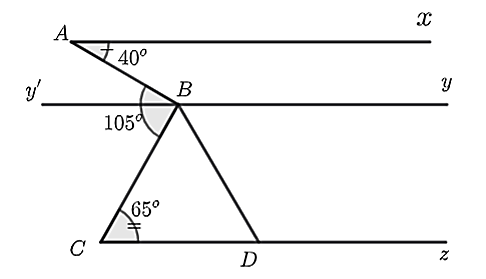
Cho hình vẽ biết \[Ax\parallel By\], \[\widehat {xAO} = 35^\circ ,\widehat {OBy} = 145^\circ \].
![Cho hình vẽ biết \[Ax\parallel By\], \[\widehat {xAO} = 35^\circ ,\widehat {OBy} = 145^\circ \]. Hỏi số đo \[\widehat {AOB}\] bằng bao nhiêu độ? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/21-1758544877.png)
Hỏi số đo \[\widehat {AOB}\] bằng bao nhiêu độ?
Cho hình vẽ biết \[Ax\parallel By\], \[\widehat {xAO} = 35^\circ ,\widehat {OBy} = 145^\circ \].
Hỏi số đo \[\widehat {AOB}\] bằng bao nhiêu độ?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: 70
Qua \[O\] kẻ đường thẳng \[tz\] song song với \[Ax\]. Suy ra \[tz\parallel By\].
![Cho hình vẽ biết \[Ax\parallel By\], \[\widehat {xAO} = 35^\circ ,\widehat {OBy} = 145^\circ \]. Hỏi số đo \[\widehat {AOB}\] bằng bao nhiêu độ? (ảnh 2)](https://video.vietjack.com/upload2/quiz_source1/2025/09/22-1758544895.png)
Vì \[tz\parallel Ax\] nên \[\widehat {xAO} = \widehat {AOz} = 35^\circ \] (so le trong)
Vì \[tz\parallel By\] nên \[\widehat {tOB} = \widehat {OBy} = 145^\circ \] (so le trong).
Mà \[\widehat {tOB}\] và \[\widehat {OBy}\] là hai góc kề bù nên ta có: \[\widehat {tOB} + \widehat {OBy} = 180^\circ \]
Suy ra \[\widehat {OBy} = 180^\circ - \widehat {tOB} = 180^\circ - 145^\circ = 35^\circ \].
Do đó, \[\widehat {zOA} + \widehat {zOB} = \widehat {AOB}\] hay \[\widehat {AOB} = 35^\circ + 35^\circ = 70^\circ \].
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) \(\frac{1}{9} - 0,3 \cdot \frac{5}{9} + \frac{1}{3} + 5\)
\( = \frac{1}{9} - \frac{3}{{10}} \cdot \frac{5}{9} + \frac{1}{3} + 5\)
\( = \frac{1}{9} - \frac{1}{6} + \frac{1}{3} + 5\)
\( = \frac{2}{{18}} - \frac{3}{{18}} + \frac{6}{{18}} + \frac{{90}}{{18}}\)\( = \frac{{95}}{{18}}\).Lời giải
k) \({\left( {\frac{3}{5}} \right)^{10}}.{\left( {\frac{5}{3}} \right)^{10}} - \frac{{{{13}^4}}}{{{{39}^4}}} + {2014^0}\)
\( = {\left( {\frac{3}{5}.\frac{5}{3}} \right)^{10}} - {\left( {\frac{{13}}{{39}}} \right)^4} + 1\)
\( = 1 - {\left( {\frac{1}{3}} \right)^4} + 1\)
\( = \frac{{2.81 - 1}}{{81}} = \frac{{161}}{{81}}\).Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo