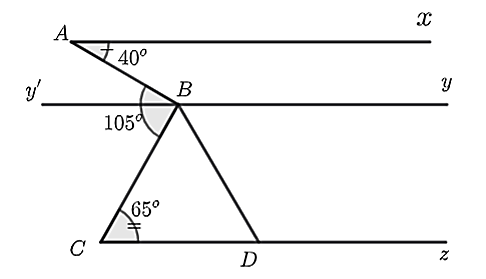
Cho hình vẽ, biết \[\widehat {mAB} = 60^\circ ,\]\[\widehat {DBe} = 75^\circ \]; \[\widehat {ACD} = 60^\circ \].
![Cho hình vẽ, biết \[\widehat {mAB} = 60^\circ ,\]\[\widehat {DBe} = 75^\circ \]; \[\widehat {ACD} = 60^\circ \]. Hỏi số đo \[\widehat {CDt}\] bằng bao nhiêu độ? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/24-1758544948.png)
Hỏi số đo \[\widehat {CDt}\] bằng bao nhiêu độ?
Cho hình vẽ, biết \[\widehat {mAB} = 60^\circ ,\]\[\widehat {DBe} = 75^\circ \]; \[\widehat {ACD} = 60^\circ \].
Hỏi số đo \[\widehat {CDt}\] bằng bao nhiêu độ?
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Đáp án: 105
Nhận thấy \[\widehat {mAB} = \widehat {ACD} = 60^\circ \] (gt) mà hai góc ở vị trí đồng vị nên \[AB\parallel CD\].
Ta có \[\widehat {DBe},\widehat {DBA}\] là hai góc kề bù nên \[\widehat {DBe} + \widehat {DBA} = 180^\circ \].
Suy ra \[\widehat {DBA} = 180^\circ - \widehat {DBe} = 180^\circ - 75^\circ = 105^\circ \].
Vì \[AB\parallel CD\] nên \[\widehat {ABD} = \widehat {CDt} = 105^\circ \].
Vậy \[\widehat {CDt} = 105^\circ \].
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) \(\frac{1}{9} - 0,3 \cdot \frac{5}{9} + \frac{1}{3} + 5\)
\( = \frac{1}{9} - \frac{3}{{10}} \cdot \frac{5}{9} + \frac{1}{3} + 5\)
\( = \frac{1}{9} - \frac{1}{6} + \frac{1}{3} + 5\)
\( = \frac{2}{{18}} - \frac{3}{{18}} + \frac{6}{{18}} + \frac{{90}}{{18}}\)\( = \frac{{95}}{{18}}\).Lời giải
k) \({\left( {\frac{3}{5}} \right)^{10}}.{\left( {\frac{5}{3}} \right)^{10}} - \frac{{{{13}^4}}}{{{{39}^4}}} + {2014^0}\)
\( = {\left( {\frac{3}{5}.\frac{5}{3}} \right)^{10}} - {\left( {\frac{{13}}{{39}}} \right)^4} + 1\)
\( = 1 - {\left( {\frac{1}{3}} \right)^4} + 1\)
\( = \frac{{2.81 - 1}}{{81}} = \frac{{161}}{{81}}\).Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo