Tìm ba số tự nhiên, biết rằng bội chung nhỏ nhất của chúng là \(540\) và ba số này tỉ lệ nghịch với \(5\,;\,\,6\) và \(15.\)
Tìm ba số tự nhiên, biết rằng bội chung nhỏ nhất của chúng là \(540\) và ba số này tỉ lệ nghịch với \(5\,;\,\,6\) và \(15.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
Gọi ba số tự nhiên cần tìm là \(x,y,z\) với \(\left( {x,y,z \in {\mathbb{N}^ * }} \right)\).
Vì ba số tỉ lệ nghịch với \(5,6\) và \(15\) nên ta có: \(5x = 6y = 15z\) suy ra \(\frac{{5x}}{{30}} = \frac{{6y}}{{30}} = \frac{{15z}}{{30}}\) hay \(\frac{x}{6} = \frac{y}{5} = \frac{z}{2}\).
Đặt \(\frac{x}{6} = \frac{y}{5} = \frac{z}{2} = k\) suy ra \(x = 6k\,;\,\,y = 5k\,;\,\,z = 2k\).
Ta có: \(BCNN(x,y,z) = 30k = 540\) suy ra \(k = 18.\)
Suy ra \(x = 6.18 = 108\,;\,\,y = 5.18 = 90\,;\,\,z = 2.18 = 36\) (thỏa mãn)
Vậy ba số tự nhiên lần lượt là: \(108\,;\,\,90\,;\,\,36\).
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
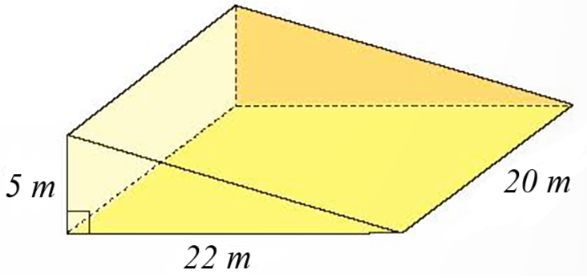
Thể tích của khối bê tông là \(20.\left( {\frac{1}{2}.5.22} \right) = 1100{\rm{ }}\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).
Vậy thể tích của khối bê tông là \(1100{\rm{ }}\,{{\rm{m}}^{\rm{2}}}.\)
Lời giải
a) Các cặp góc đối đỉnh là \(\widehat {xAy}\) và \(\widehat {x'Ay'}\) ; \(\widehat {x'Ay}\) và \(\widehat {xAy'}\).
b) Các cặp góc kề bù là \(\widehat {xAy}\) và \(\widehat {x'Ay}\); \(\widehat {xAy}\) và \(\widehat {xAy'}\); \(\widehat {x'Ay}\) và \(\widehat {x'Ay'}\); \(\widehat {x'Ay'}\) và \(\widehat {xAy'}\).
c) Ta có tia \(At\) là tia phân giác của \(\widehat {xAy}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Cho hình vẽ bên có \[\widehat {xOM} = \widehat {yON} = 30^\circ ,\,\,OI\] là tia phân giác của góc \[MON\]. Hai đường thẳng \[OI,xy\] có vuông góc với nhau hay không? (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/09/31-1758546744.png)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo