Một cái lều có dạng hình lăng trụ đứng tam giác \(ABC.A'B'C'\) với các số đo như hình vẽ.

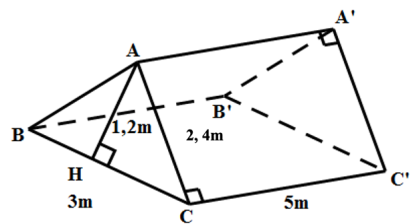
a) Cô giáo muốn giao cho các bạn lớp 7A tự làm lều và các bạn được cung cấp 200 m vải. Biết các mặt cần dùng vải là \(ABC,\,\,A'B'C',\,\,ABB'A',\,\,ACC'A'\). Hỏi với 200 mét vải dựng được bao nhiêu cái lều.

b) Biết không gian dành cho 1 bạn học sinh là \(4{\rm{ }}{{\rm{m}}^3}\). Hỏi mỗi lều có thể chứa tối đa bao nhiêu học sinh?

Hướng dẫn giải

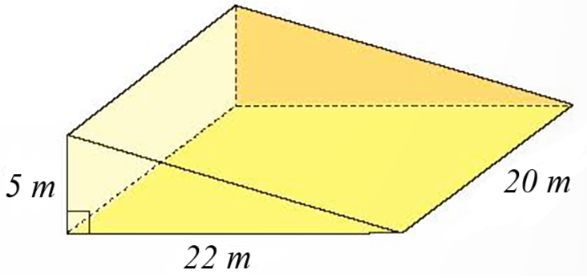
Thể tích của khối bê tông là \(20.\left( {\frac{1}{2}.5.22} \right) = 1100{\rm{ }}\,\left( {{{\rm{m}}^{\rm{2}}}} \right)\).

Vậy thể tích của khối bê tông là \(1100{\rm{ }}\,{{\rm{m}}^{\rm{2}}}.\)

a) Các cặp góc đối đỉnh là \(\widehat {xAy}\) và \(\widehat {x'Ay'}\) ; \(\widehat {x'Ay}\) và \(\widehat {xAy'}\).

b) Các cặp góc kề bù là \(\widehat {xAy}\) và \(\widehat {x'Ay}\); \(\widehat {xAy}\) và \(\widehat {xAy'}\); \(\widehat {x'Ay}\) và \(\widehat {x'Ay'}\); \(\widehat {x'Ay'}\) và \(\widehat {xAy'}\).

c) Ta có tia \(At\) là tia phân giác của \(\widehat {xAy}\).