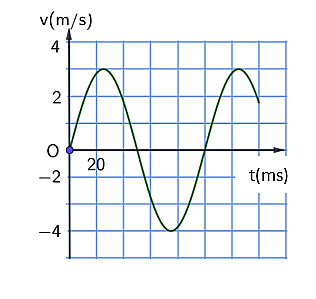
Một chất điểm dao động điều hòa có vận tốc cực đại \(40\pi {\rm{cm}}/{\rm{s}}\) và gia tốc cực đại \(3,2{\pi ^2}\;{\rm{m}}/{{\rm{s}}^2}\). Chọn mốc thế năng tại vị trí cân bằng. Thời điểm ban đầu \(({\rm{t}} = 0)\), chất điểm có vận tốc \({\rm{v}} = - 20\pi \)cm/s và thế năng đang tăng. Chất điểm đi qua vị trí cân bằng lần thứ 2021 vào thời điểm bao nhiêu giây? Kết quả làm tròn đến phần nguyên.
Đáp án:
Một chất điểm dao động điều hòa có vận tốc cực đại \(40\pi {\rm{cm}}/{\rm{s}}\) và gia tốc cực đại \(3,2{\pi ^2}\;{\rm{m}}/{{\rm{s}}^2}\). Chọn mốc thế năng tại vị trí cân bằng. Thời điểm ban đầu \(({\rm{t}} = 0)\), chất điểm có vận tốc \({\rm{v}} = - 20\pi \)cm/s và thế năng đang tăng. Chất điểm đi qua vị trí cân bằng lần thứ 2021 vào thời điểm bao nhiêu giây? Kết quả làm tròn đến phần nguyên.
|
Đáp án: |
|
|
|
|
Câu hỏi trong đề: Đề kiểm tra Vật Lí 11 Cánh diều Chủ đề 1 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
\(\omega = \frac{{{a_{\max }}}}{{{v_{\max }}}} = \frac{{320{\pi ^2}}}{{40\pi }} = 8\pi \) (rad/s)
\(v = - \frac{{{v_{\max }}}}{2}\) và thế năng tăng\( \Rightarrow x = - \frac{{A\sqrt 3 }}{2}\) theo chiều âm\( \Rightarrow \varphi = \frac{{5\pi }}{6}\)
\({t_{2021}} = \frac{\alpha }{\omega } = \frac{{2020\pi + \frac{\pi }{6} + \frac{\pi }{2}}}{{8\pi }} = \frac{{3031}}{{12}}s \approx 253s\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
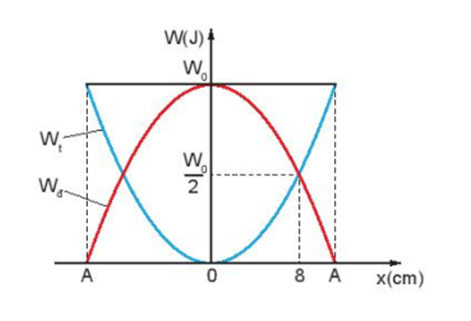
- Dựa vào đồ thị: Tại \(x = 8\left( {cm} \right)\)ta có \({{\rm{W}}_d} = {{\rm{W}}_t} = \frac{{{{\rm{W}}_0}}}{2}\)
- Do đó: \(\left| x \right| = \frac{A}{{\sqrt 2 }} \Leftrightarrow A = 8\sqrt 2 \left( {cm} \right)\)
- Cơ năng của con lắc: \[{{\rm{W}}_0} = \frac{1}{2}k{A^2} = 0,64\left( J \right)\]
Câu 2
A. \(\frac{{2\pi }}{3}\,rad\).
B. \(\frac{\pi }{3}\,rad\).
C. \( - \frac{\pi }{3}\,\,rad\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn đáp án B
- Dao động x1: Lúc t = 0, \[x = \frac{A}{2}( - ) \Rightarrow {\varphi _1} = \frac{\pi }{3}rad\]
- Dao động x2: Lúc t = 0, \[x = - \frac{A}{2}( - ) \Rightarrow {\varphi _1} = \frac{{2\pi }}{3}rad\]
- Độ lệch pha là: \[\frac{{2\pi }}{3} - \frac{\pi }{3} = \frac{\pi }{3}rad\]
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
\(10\sqrt 3 \pi cm/s\).
\(5\pi \sqrt 3 \;cm/s\).
\(10\sqrt 2 \pi cm/s\).
\(10\pi cm/s\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập