Cho thanh thẳng AB chiều dài L = 1,5 m quay đều xung quanh trục đi qua điểm O trên thanh và vuông góc với thanh. Tốc độ của hai đầu thanh lần lượt là \({v_A} = 2\,m/s\) và \({v_B} = 4\,m/s\). Tỉ số giữa gia tốc hướng tâm tại hai điểm B và A là
A. 0,5.
B. 2.
C. 4.
D. 1,5.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn B
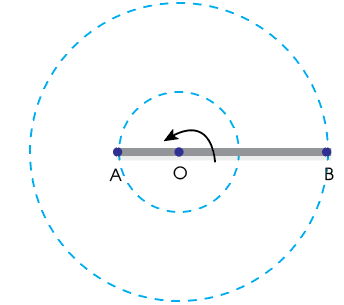
Tốc độ của điểm A: \({v_A} = \omega .{r_A}\)
Tốc độ của điểm B: \({v_B} = \omega .{r_B}\)
Ta có hệ phương trình:
\[\left\{ \begin{array}{l}\frac{{{v_A}}}{{{r_A}}} = \frac{{{v_B}}}{{{r_B}}}\\{r_A} + {r_B} = AB\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\frac{2}{{{r_A}}} = \frac{4}{{{r_B}}}\\{r_A} + {r_B} = 1,5\end{array} \right. \Rightarrow \left\{ \begin{array}{l}{r_A} = 0,5\,m\\{r_B} = 1\,m\end{array} \right.\]
Tốc độ góc của thanh là: \[\omega = \frac{{{v_A}}}{{{r_A}}} = \frac{2}{{0,5}} = 4\,rad/s\]
Gia tốc hướng tâm của điểm A: \({a_{ht\,A}} = {\omega ^2}.{r_A} = {4^2}.0,5 = 8\,m/{s^2}\)
Gia tốc hướng tâm của điểm B: \({a_{ht\,B}} = {\omega ^2}.{r_B} = {4^2}.1 = 16\,m/{s^2}\)
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Các sản phẩm khác của Vietjack:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Một vòng quay tương ứng với góc \(\theta = 2\pi \,{\rm{rad}}\)
Bán kính vòng quay là \[r = 52,5\,{\rm{m}}\]
Chiều dài quĩ đạo của mỗi điểm treo cabin khi vòng quay chuyển động được một vòng là
\[s = \theta .r = 2\pi .52,5 = 2.3,14.52,5 \approx 330\,{\rm{m}}\]
Lời giải
Hợp lực tác dụng lên (người + xe) đóng vai trò là lực hướng tâm: \(\overrightarrow {{F_{ht}}} = \overrightarrow P + \overrightarrow N \)
- Chiếu lên phương hướng tâm (phương trùng với bán kính, chiều dương hướng vào tâm quỹ đạo). Ta có:
\(\begin{array}{l}\,\,\,\,\,\,{F_{ht}} = P + N\\ \Rightarrow N = {F_{ht}} - P = m.\frac{{{v^2}}}{R} - m.g\end{array}\)
Để xe đạp không bị rơi thì N ≥ 0.
\[\begin{array}{l}m.\frac{{{v^2}}}{R} - m.g \ge 0\\ \Rightarrow v \ge \sqrt {R.g} \\ \Rightarrow {v_{\min }} = \sqrt {R.g} = \sqrt {6,4.10} = 8\,m/s\end{array}\]
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. 33,5 rad/s.
B. 41,87 rad/s.
C. 48,7 rad/s.
D. 35,3 rad/s.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập