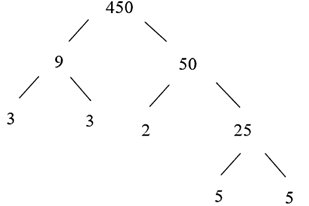
Cho \({a^2} \cdot b \cdot 7 = 140\) với \(a,b\) là các số nguyên tố.
Cho \({a^2} \cdot b \cdot 7 = 140\) với \(a,b\) là các số nguyên tố.
Giá trị của \(a\) là
1.
2.
3.
4.
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn đáp án B
Ta có: \(140 = {2^2} \cdot 5 \cdot 7\).
Mà \({a^2} \cdot b \cdot 7 = 140\) nên \({a^2} \cdot b \cdot 7 = {2^2} \cdot 5 \cdot 7\).
Do đó, \(a = 2\).
Câu hỏi cùng đoạn
Câu 2:
Giá trị của \(b\) là
1.
2.
5.
7.
Giải bởi Vietjack
Chọn đáp án C
Vì \({a^2} \cdot b \cdot 7 = {2^2} \cdot 5 \cdot 7\) nên \(b = 5\).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 3
Ta có: \(84 = {2^2} \cdot 3 \cdot 7\).
Do đó, số 84 có 3 ước nguyên tố là 2; 3; 7.
Lời giải
Đáp án: 420
Nhận thấy \(420 = {2^2} \cdot 3 \cdot 5 \cdot 7\).
Do đó, số 420 có các ước nguyên tố là \(2;\,\,3;\,\,5;\,\,7\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập