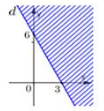
Miền nghiệm của bất phương trình \(5\left( {x + 2} \right) - 9 < 2x - 2y + 7\) không chứa điểm nào trong các điểm sau?
Câu hỏi trong đề: Đề kiểm tra Bất phương trình bậc nhất hai ẩn (có lời giải) !!
Quảng cáo
Trả lời:
Chọn A
Thay tọa độ điểm \(\left( {2\,;\,\,3} \right)\) vào bất phương trình \(5\left( {x + 2} \right) - 9 < 2x - 2y + 7\) ta có:
\(5\left( {2 + 2} \right) - 9 < 2.2 - 2.3 + 7 \Leftrightarrow 11 < 5\).
Vậy miền nghiệm của bất phương trình \(5\left( {x + 2} \right) - 9 < 2x - 2y + 7\) không chứa điểm \(\left( {2\,;\,\,3} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Văn, Anh 10 cho cả 3 bộ KNTT, CTST, CD VietJack - Sách 2025 ( 13.600₫ )
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi \(x,y\) (chiếc) là số lượng bánh nướng, bánh dẻo mà xí nghiệp cần sản xuất. Trong đó \(0 < x,0 < y\) với \(x,y \in {\mathbb{N}^*}\).
Khối lượng bột mỳ cần dùng là: \(0,12x + 0,16y(\;kg)\).
Khối lượng đường cần dùng là: \(0,06x + 0,04y(\;kg)\).
Ta có: \(0,12x + 0,16y \le 600\) hay \(3x + 4y \le 15000\);
\(0,06x + 0,04y \le 240\) hay \(3x + 2y \le 12000\).
Số tiền lãi thu được là: \(T = 8x + 6y\) (nghìn đồng). Bài toán đưa về, tìm \(x,y\) là nghiệm của hệ bất phương trình: \(\left\{ \begin{array}{l}3x + 4y \le 15000\\3x + 2y \le 1200\\y \le 3x\\x \ge 0\\y \ge 0\end{array} \right.\left( V \right)\) để \(T = 8x + 6y\) đạt giá trị lớn nhất.
Trước hết, ta biểu diễn miền nghiệm của hệ bất phương trình (V).
Miền nghiệm của hệ bất phương trình là miền tứ giác \(OABC\) với \(O\left( {0;0} \right),\,A\left( {4000;0} \right),B\left( {3000;1500} \right),\,C\left( {1000;3000} \right)\)
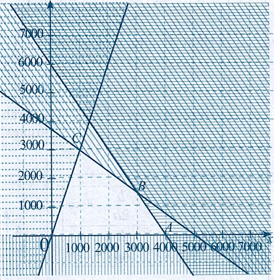
Tính giá trị của \(T\) tại các cặp số \((x;y)\) là toạ độ các đỉnh trên rồi so sánh các giá trị đó, ta được \(T\) đạt giá trị lớn nhất bằng 33000 (nghìn đồng) hay 33 triệu đồng tại \(x = 3000;y = 1500\).
Vậy để đạt được tiền lãi cao nhất, xí nghiệp nên sản xuất 3000 chiếc bánh nướng và \(1.500\) chiếc bánh dẻo.
Lời giải
Gọi \(x,y\) lần lượt là số ki-lô-gam thịt bò và thịt lợn mà gia đình đó mua trong một ngày với \(0 \le x \le 1,6,0 \le y \le 1,1\).
Số đơn vị protein gia đình có là: \(800x + 600y\).
Số đơn vị lipit gia đình có là: \(200x + 400y\). Theo bài ra, ta có:
\(\left\{ {\begin{array}{*{20}{l}}\begin{array}{l}0 \le x \le 1,6\\0 \le y \le 1,1\\800x + 600y \ge 900\\200x + 400y \ge 400\end{array}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}\begin{array}{l}0 \le x \le 1,6\\0 \le y \le 1,1\\8x + 6y \ge 9\\x + 2y \ge 2\end{array}\end{array}} \right.} \right.\left( {IV} \right)\)
Số tiền gia đình đã dùng để mua thịt bò và thịt lợn là:
\[T = 200000{\rm{ }}x + 160000{\rm{ }}y\](đồng).
Bài toán đưa về tìm \(x,y\) là nghiệm của hệ bất phương trình (IV) để \(T = 200000x + 160000y\) đạt giá trị nhỏ nhất.
Trước hết, ta biểu diễn miền nghiệm của hệ bất phương trình (IV).
Miền nghiệm của hệ bất phương trình (IV) là miền tứ giác \(ABCD\) với \(A(0,3;1,1),B(0,6;0,7),C(1,6;0,2)\), \(D(1,6;1,1)\)(hình)
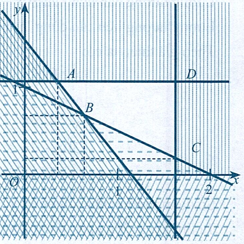
Tính giá trị của \(T\) tại các cặp số \((x;y)\) là tọa độ của các đỉnh tứ giác \(ABCD\) rồi so sánh các giá trị đó, ta được \(T\) đạt giá trị nhỏ nhất bằng 232000 đồng tại \(x = 0,6;y = 0,7\)
Vậy để đảm bảo cung cấp đủ lượng protein, lipit cho gia đình và có chi phí là ít nhất thì gia đình đó cần mua thêm \(0,6kg\) thịt bò và \(0,7kg\)thịt lợn
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.