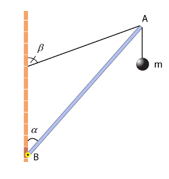
Vật m =2 kg treo trên trần và tường bằng các dây AB, AC. Lực căng dây của dây AC là bao nhiêu N? biết \(\alpha = {60^0};\beta = {135^0}.\) Lấy g = 10 m/s2. ( Kết quả lấy đến 3 chữ số có nghĩa)
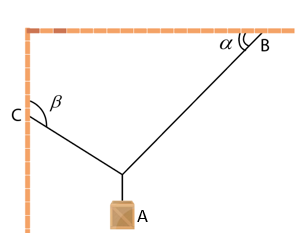
Vật m =2 kg treo trên trần và tường bằng các dây AB, AC. Lực căng dây của dây AC là bao nhiêu N? biết \(\alpha = {60^0};\beta = {135^0}.\) Lấy g = 10 m/s2. ( Kết quả lấy đến 3 chữ số có nghĩa)
Quảng cáo
Trả lời:
Giải bởi Vietjack
|
Đáp án: |
1 |
0 |
, |
6 |
- Chọn hệ tọa độ như hình vẽ
- Vật nằm cân bằng nên: \({\vec T_1} + {\vec T_2} + \vec P = \vec 0\left( 1 \right)\)
- Chiếu (1)/Oy, ta có:
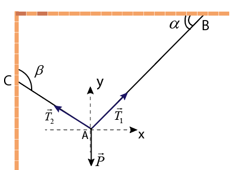
\({T_2}\cos \left( {{{180}^0} - \beta } \right) + {T_1}\cos \left( {{{90}^0} - \alpha } \right) - P = 0\left( 2 \right)\)
- Chiếu (1)/Ox, ta có:
\(\begin{array}{l}{T_1}\sin \left( {{{90}^0} - \alpha } \right) - {T_2}\sin \left( {{{180}^0} - \beta } \right) = 0\left( 3 \right)\\ = > {T_1} = \frac{{{T_2}\sin \left( {{{180}^0} - \beta } \right)}}{{\sin \left( {{{90}^0} - \alpha } \right)}} = \frac{{{T_2}\sin {{45}^0}}}{{\sin {{30}^0}}}\end{array}\)
Thay vào (2) tao có:
\(\begin{array}{l}{T_2}\cos {45^0} + {T_2}\frac{{\sin {{45}^0}}}{{\sin {{30}^0}}}\cos {30^0} = P\\ \Leftrightarrow {T_2} = \frac{{mg}}{{\cos {{45}^0} + \sin {{45}^0}\cot {{30}^0}}} = \frac{{2.10}}{{\frac{{\sqrt 2 }}{2} + \frac{{\sqrt 2 }}{2}.\sqrt 3 }} = 10,6N\end{array}\)
Hot: 1000+ Đề thi giữa kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
|
Đáp án: |
2 |
3 |
, |
5 |
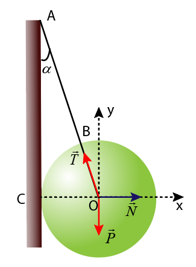
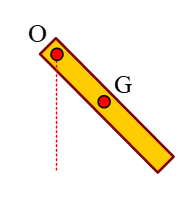
Chọn hệ Oxy như hình vẽ
- Quả cầu cân bằng nên: \(\vec P + \vec N + \vec T = \vec 0\left( 1 \right)\)
- Ta có: \[\sin \alpha = \frac{{CO}}{{AB + BO}} = \frac{R}{{AB + R}} = \frac{{15}}{{30}} = \frac{1}{2} = > \alpha = {30^0}\]
- Chiếu (1)/Oy, ta có: \( - P + T\cos \alpha = 0 = > T = \frac{P}{{\cos \alpha }} = \frac{{mg}}{{\cos \alpha }} = \frac{{4.10}}{{\cos {{30}^0}}} \simeq 47N\)
- Chiếu (2)/Ox; ta có: \(N - T\sin \alpha = 0 = > N = T\sin \alpha = 47.\sin {30^0} = 23,5N\)
Vậy lực nén lên tường \(N' = N = 23,5N\)
Lời giải
|
Đáp án: |
6 |
6 |
9 |
|
Hướng dẫn giải
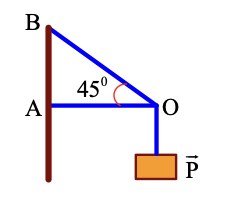
- Chọn trục Oxy như hình vẽ
- Điều kiện cân bằng: \(\vec P + \vec F + \vec T = \vec 0\left( 1 \right)\)
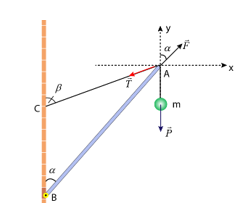
- Chiếu (1)/Oy: \(F\cos \alpha - T\cos \beta - P = 0\left( 2 \right)\)
- Chiếu (2)/Ox: \(F\sin \alpha - T\sin \beta = 0\left( 3 \right)\)
- Từ (3) => \(F = T\frac{{\sin \beta }}{{\sin \alpha }}\), thay vào (2)
Ta có:\(T\frac{{\sin \beta }}{{\sin \alpha }}\cos \alpha - T\cos \beta = P \Leftrightarrow T = \frac{P}{{\sin \beta \cot \alpha - \cos \beta }} = 546,4N\)
- Lực đàn hồi của thanh AB: \(F = T\frac{{\sin \beta }}{{\sin \alpha }} = 546,4.\frac{{\sin {{60}^0}}}{{\sin {{45}^0}}} = 669,2N\)
Câu 3
A. Hợp lực thay thế cho nhiều lực đồng thời tác dụng vào vật và cho cùng hiệu quả.
B. Tổng hợp một hệ lực tác dụng đồng thời vào vật ta dùng quy tắc đa giác lực hay dùng nối tiếp quy tắc hình bình hành.
C. Phép tổng hợp lực là ngược lại với phép phân tích lực.
D. Một lực tác dụng chỉ có thể phân tích thành một cặp lực thành phần duy nhất vuông góc với nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. 7\(\sqrt 3 \)N.
B. \(10\sqrt {73} \)N.
C. \(3\sqrt 7 \) N.
D. \(73\sqrt {10} \) N.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo