Một viên đạn có khối lượng \(3{\rm{\;kg}}\) đang rơi tự do, \(2{\rm{\;s}}\) sau khi rơi thì nổ thành hai mảnh có khối lượng gấp 2 lần nhau. Lấy \({\rm{g}} = 10{\rm{\;m}}/{{\rm{s}}^2}\). Nếu mảnh nhỏ bay theo phương ngang với vận tốc \(20\sqrt 3 {\rm{\;m}}/{\rm{s}}\) thì vận tốc của mảnh còn lại

- Thời gian đạn nổ là rất ngắn nên có thể coi hệ là kín.

- Tốc độ của đạn trước khi nổ xác định theo các công thức rơi tự do: \({\rm{v}} = \) g.t.

- Sau khi nổ hai mảnh của đạn chuyển động với vận tốc \({{\rm{\vec v}}_1}\) và \({{\rm{\vec v}}_2}\) với \({{\rm{\vec v}}_1} \bot {\rm{\vec v}}\).

Lời giải: Chọn A.

     Xét hệ kín gồm hai mảnh đạn có khối lượng là \({{\rm{m}}_1}\) và \({{\rm{m}}_2}\).

     Ta có: \(\left[ {\begin{array}{*{20}{l}}{{{\rm{m}}_2} = 2{\rm{\;}}{{\rm{m}}_1}}\\{{{\rm{m}}_2} + {{\rm{m}}_1} = 3{\rm{\;kg}}}\end{array} \Rightarrow \left[ {\begin{array}{*{20}{l}}{{{\rm{m}}_1} = 1{\rm{\;kg}}}\\{{{\rm{m}}_2} = 2{\rm{\;kg}}}\end{array}} \right.} \right.\)

Tốc độ của viên đạn ngay trước khi nổ là: \({\rm{v}} = {\rm{g}}{\rm{.t}} = 10.2 = 20{\rm{\;m}}/{\rm{s}}\).

Động lượng của hệ trước khi đạn nổ: \({\rm{\vec p}} = \left( {{{\rm{m}}_1} + {{\rm{m}}_2}} \right){\rm{\vec v}}\).

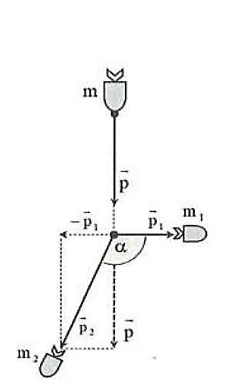
Động lượng của hệ sau khi đạn nổ: \({{\rm{\vec p}}^{\rm{'}}} = {{\rm{\vec p}}_1} + {{\rm{\vec p}}_2} = {{\rm{m}}_1}{\rm{.}}{{\rm{\vec v}}_1} + {{\rm{m}}_2}{\rm{.}}{{\rm{\vec v}}_2}\).

     Áp dụng định luật bảo toàn động lượng ta có: \({\rm{\vec p}} = {{\rm{\vec p}}_1} + {{\rm{\vec p}}_2} \Leftrightarrow {\rm{\vec p}} - {{\rm{\vec p}}_1} = {{\rm{\vec p}}_2}\).

     \({\rm{\vec p}} \bot {{\rm{\vec p}}_1} \Rightarrow {{\rm{p}}_2} = \sqrt {{{\rm{p}}^2} + {\rm{p}}_1^2} \)

     \(\left\langle {\begin{array}{*{20}{l}}{{\rm{p}} = {\rm{mv}} = 3.20 = 60{\rm{\;kg}}{\rm{.m/s}}}\\{{{\rm{p}}_1} = {{\rm{m}}_1}{{\rm{v}}_1} = 1.20\sqrt 3  = 20\sqrt 3 {\rm{\;kg}}{\rm{.m/s}}}\end{array}} \right. \Rightarrow {{\rm{p}}_2} = \sqrt {{{60}^2} + {{(20\sqrt 3 )}^2}}  = 40\sqrt 3 {\rm{\;kg}}{\rm{.m/s}}\).

     \( \Rightarrow {{\rm{v}}_2} = \frac{{{{\rm{p}}_2}}}{{{\rm{\;}}{{\rm{m}}_2}}} = \frac{{40\sqrt 3 }}{2} = 20\sqrt 3 {\rm{\;m}}/{\rm{s}}\).

     Gọi \(\alpha  = \left( {{{{\rm{\vec p}}}_1};{{{\rm{\vec p}}}_2}} \right) \Rightarrow {{\rm{p}}^2} = {\rm{p}}_1^2 + {\rm{p}}_2^2 + 2{{\rm{p}}_1}{{\rm{p}}_2}{\rm{.cos}}\alpha \).

     \( \Rightarrow {\rm{cos}}\alpha  = \frac{{{{60}^2} - \left[ {{{(20\sqrt 3 )}^2} + {{(40\sqrt 3 )}^2}} \right]}}{{2.20\sqrt 3 .40\sqrt 3 }} =  - \frac{1}{2} \Rightarrow \alpha  = {120^ \circ }{\rm{.\;}}\)

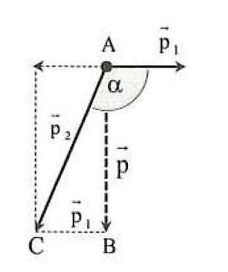
 Nhận xét:  Ta có thể giải bằng phương pháp hình học như sau:

     Xét tam giác \({\rm{ABC}}\) ta có: \({\rm{tan}}\widehat {{\rm{CAB}}} = \frac{{{{\rm{p}}_1}}}{{\rm{p}}} = \frac{{20\sqrt 3 }}{{60}}\)

     \( \Rightarrow \widehat {{\rm{CAB}}} = {30^ \circ } \Rightarrow \alpha  = {90^ \circ } + \widehat {{\rm{CAB}}} = {120^ \circ }\)     \({\rm{sin}}\widehat {{\rm{CAB}}} = \frac{{{{\rm{p}}_1}}}{{{{\rm{p}}_2}}} \Leftrightarrow {\rm{sin}}{30^ \circ } = \frac{{20\sqrt 3 }}{{{{\rm{p}}_2}}} \Rightarrow {{\rm{p}}_2} = 40\sqrt 3 {\rm{\;kg}}{\rm{.m/s}} \Rightarrow {{\rm{v}}_2} = \frac{{{{\rm{p}}_2}}}{{{\rm{\;}}{{\rm{m}}_2}}} = \frac{{40\sqrt 3 }}{2} = 20\sqrt 3 {\rm{\;m/s}}.\)