Một hình chóp tứ giác đều \(S.ABCD\) có thể tích bằng \(200\;\,{\rm{c}}{{\rm{m}}^3}.\) Gọi \(M,\;\,N,\;\,P,\;\,Q\) lần lượt là trung điểm của \(AB,\;\,BC,\;\,CD,\;\,DA.\) Biết rằng \(SO\) là đường cao của hai hình chóp \(S.ABCD\)và \(S.MNPQ.\) Tính thể tích của hình chóp \(S.MNPQ\) (Đơn vị: \({\rm{c}}{{\rm{m}}^3}\)).
Một hình chóp tứ giác đều \(S.ABCD\) có thể tích bằng \(200\;\,{\rm{c}}{{\rm{m}}^3}.\) Gọi \(M,\;\,N,\;\,P,\;\,Q\) lần lượt là trung điểm của \(AB,\;\,BC,\;\,CD,\;\,DA.\) Biết rằng \(SO\) là đường cao của hai hình chóp \(S.ABCD\)và \(S.MNPQ.\) Tính thể tích của hình chóp \(S.MNPQ\) (Đơn vị: \({\rm{c}}{{\rm{m}}^3}\)).
Quảng cáo
Trả lời:
Giải bởi Vietjack
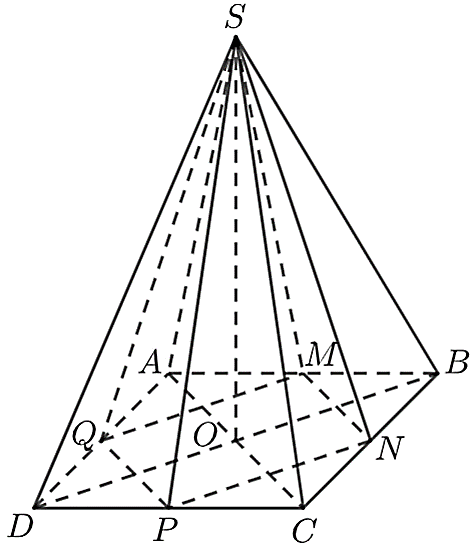
Vì \(S.ABCD\) là hình chóp tứ giác đều nên \(ABCD\) là hình vuông. Do đó, \(AB = BC = CD = DA.\)
Vì \(M,\;\,N,\;\,P,\;\,Q\) lần lượt là trung điểm của \(AB,\;\,BC,\;\,CD,\;\,DA\) nên
\(MA = MB = NB = NC = PC = DP = QD = QA = \frac{1}{2}CB.\)
Vì \(\Delta AMQ = \Delta BMN = \Delta CPN = \Delta DPQ\;\;\left( {cgv - cgv} \right)\) nên \({S_{\Delta AMQ}} = {S_{\Delta BMN}} = {S_{\Delta CPN}} = {S_{\Delta DPQ}}.\)
Do đó: \({S_{MNPQ}} = {S_{ABCD}} - 4{S_{\Delta MNB}} = C{B^2} - 4 \cdot \frac{1}{2}MB \cdot NB = C{B^2} - 2{\left( {\frac{1}{2}CB} \right)^2} = \frac{1}{2}C{B^2} = \frac{1}{2}{S_{ABCD}}.\)
Mà hai hình chóp \(S.ABCD\)và \(S.MNPQ\) có cùng chiều cao \(SO.\)
Do đó, \({V_{S.MNPQ}} = \frac{1}{2}{V_{S.ABCD}} = \frac{1}{2} \cdot 200 = 100\;\,\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)
Vậy thể tích của hình chóp \(S.MNPQ\) bằng \(100\;{\rm{c}}{{\rm{m}}^3}.\)
Hot: Học hè online Toán, Văn, Anh...lớp 1-12 tại Vietjack với hơn 1 triệu bài tập có đáp án. Học ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 500
Thể tích của hộp quà lưu niệm là: \(\frac{1}{3} \cdot {10^2} \cdot 15 = 500\;\,\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)
Vậy thể tích của hộp quà lưu niệm là \(500\;\,{\rm{c}}{{\rm{m}}^3}.\)
Lời giải
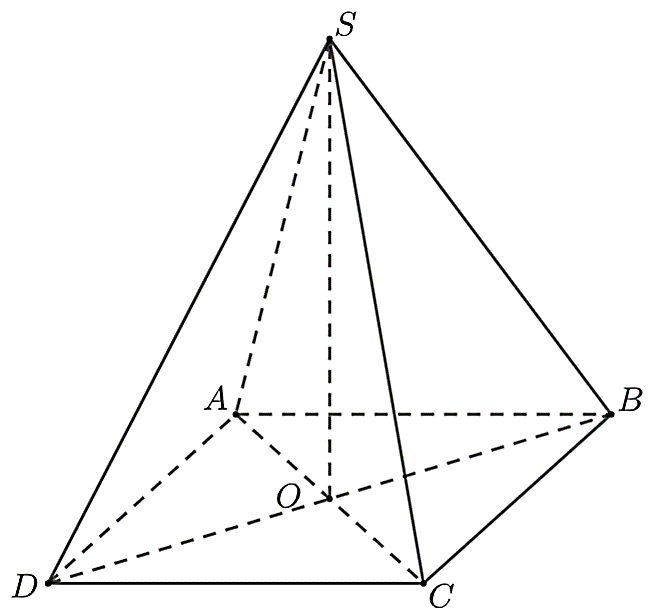
a) Đúng.
Vì \(O\) là tâm của hình vuông \(ABCD\) nên \(O\) là giao điểm của hai đường chéo trong hình vuông \(ABCD.\) Vậy \(SO\) là đường cao của hình chóp \(S.ABCD.\)
b) Đúng.
Vì hình vuông \(ABCD\) có chu vi bằng \(24\;\,{\rm{cm}}\) nên \(4AB = 24\) nên \(AB = 6\;\,{\rm{cm}}{\rm{.}}\)
Do đó, \(SO = \frac{2}{3}AB = \frac{2}{3} \cdot 6 = 4\;\,\left( {{\rm{cm}}} \right).\) Vậy \(SO = 4\;\,{\rm{cm}}{\rm{.}}\)
c) Đúng.
Diện tích của hình vuông \(ABCD\) là: \(A{B^2} = {6^2} = 36\;\,{\rm{c}}{{\rm{m}}^2}.\)
Vậy diện tích hình vuông \(ABCD\) bằng \(36\;\,{\rm{c}}{{\rm{m}}^2}.\)
d) Sai.
Thể tích hình chóp tứ giác \(S.ABCD\) là: \(V = \frac{1}{3} \cdot 4 \cdot 36 = 48\;\left( {{\rm{c}}{{\rm{m}}^3}} \right).\)
Vậy thể tích của hình chóp \(S.ABCD\) bằng \(48\;\,{\rm{c}}{{\rm{m}}^3}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Hình tam giác đều.
B. Hình vuông.
C. Hình thoi.
D. Hình tam giác cân.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(SO.\)
B. \(OE.\)
C. \(SE.\)
D. \(SB.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
A. \(120\,\;{\rm{c}}{{\rm{m}}^2}.\)
B. \(120\;\,{\rm{c}}{{\rm{m}}^3}.\)
C. \(40\;\,{\rm{c}}{{\rm{m}}^3}.\)
D. \(40\;\,{\rm{c}}{{\rm{m}}^2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo