Một hình chóp tứ giác đều có thể tích là \({V_1}.\) Nếu giữ nguyên chiều cao của hình chóp đó và tăng độ dài cạnh đáy lên 5 lần thì được một hình chóp mới có thể tích là \({V_2}.\) Tính \(\frac{{{V_2}}}{{{V_1}}}.\)

a) Đúng.

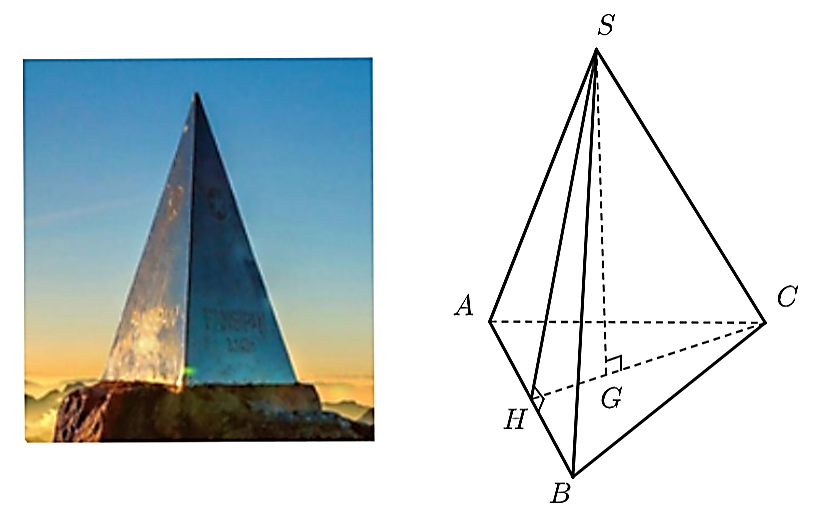
Mặt đáy của hình chóp \(S.ABC\) là một tam giác đều \(ABC\) có cạnh \(60{\rm{ cm}}{\rm{.}}\) Gọi đường cao của mặt đáy là \(CH\), ta có \(CH\) đồng thời là đường trung tuyến.

\(HA = HB = \frac{{AB}}{2} = 30{\rm{ cm}}{\rm{.}}\)

b) Đúng.

Xét tam giác \(BHC\) vuông tại \(H\). Theo định lý Pythagore ta có: \(C{B^2} = H{B^2} + H{C^2}\) hay \({60^2} = {30^2} + H{C^2}\) suy ra \(C{H^2} = {60^2} - {30^2} = 2{\rm{ }}700\) nên \(CH = \sqrt {2700} = 30\sqrt 3 {\rm{ }}\left( {{\rm{cm}}} \right)\).

c) Sai.

Vì \(G\) là trọng tâm của mặt đáy nên \(GH = \frac{1}{3}HC = \frac{{30\sqrt 3 }}{3} = 10\sqrt 3 {\rm{ }}\left( {{\rm{cm}}} \right)\).

Hình chóp \(S.ABC\) có đường cao \(SG\) nên \(SG \bot HC.\)

Xét tam giác \(SHG\) vuông tại \(G\). Theo định lý Pythagore, ta có:

\(S{H^2} = S{G^2} + H{G^2}\)

\(S{H^2} = {90^2} + {30^2} = 9000\)

Suy ra \(SH = \sqrt {9000} = 30\sqrt {10} {\rm{ cm}}{\rm{.}}\)

d) Đúng.

Vậy diện tích xung quanh của hình chóp là \(S = 3 \cdot \frac{1}{2} \cdot 60 \cdot 30\sqrt {10} \approx 8538{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\).

Đáp án: 520

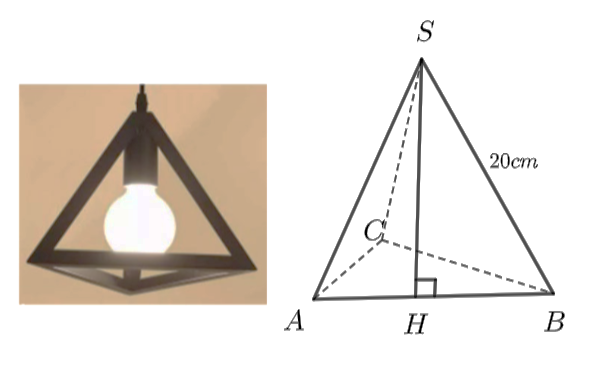
Các mặt bên và mặt đáy của hình chóp \(S.ABC\) là những tam giác đều cạnh \(20{\rm{ cm}}{\rm{.}}\)

Xét tam giác đều \(SAB\) có đường cao \(SH\) đồng thời là đường trung tuyến, ta có:

\(AH = BH = \frac{{AB}}{2} = 10{\rm{ cm}}\).

Xét tam giác \(SHB\) vuông tại \(H\). Theo định lí Pythagore, ta có:

\(S{B^2} = S{H^2} + B{H^2}\) hay \({20^2} = S{H^2} + {10^2}\) suy ra \(S{H^2} = S{B^2} - B{H^2} = 300\).

Suy ra \(SH = \sqrt {300} \approx 17,32{\rm{ }}\left( {{\rm{cm}}} \right)\).

Diện tích xung quanh của hình chóp tam giác đều \(S.ABC\) là:

\({S_{xq}} = 3 \cdot \frac{1}{2} \cdot 30 \cdot 17,32 = 519,6 \approx 520{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).