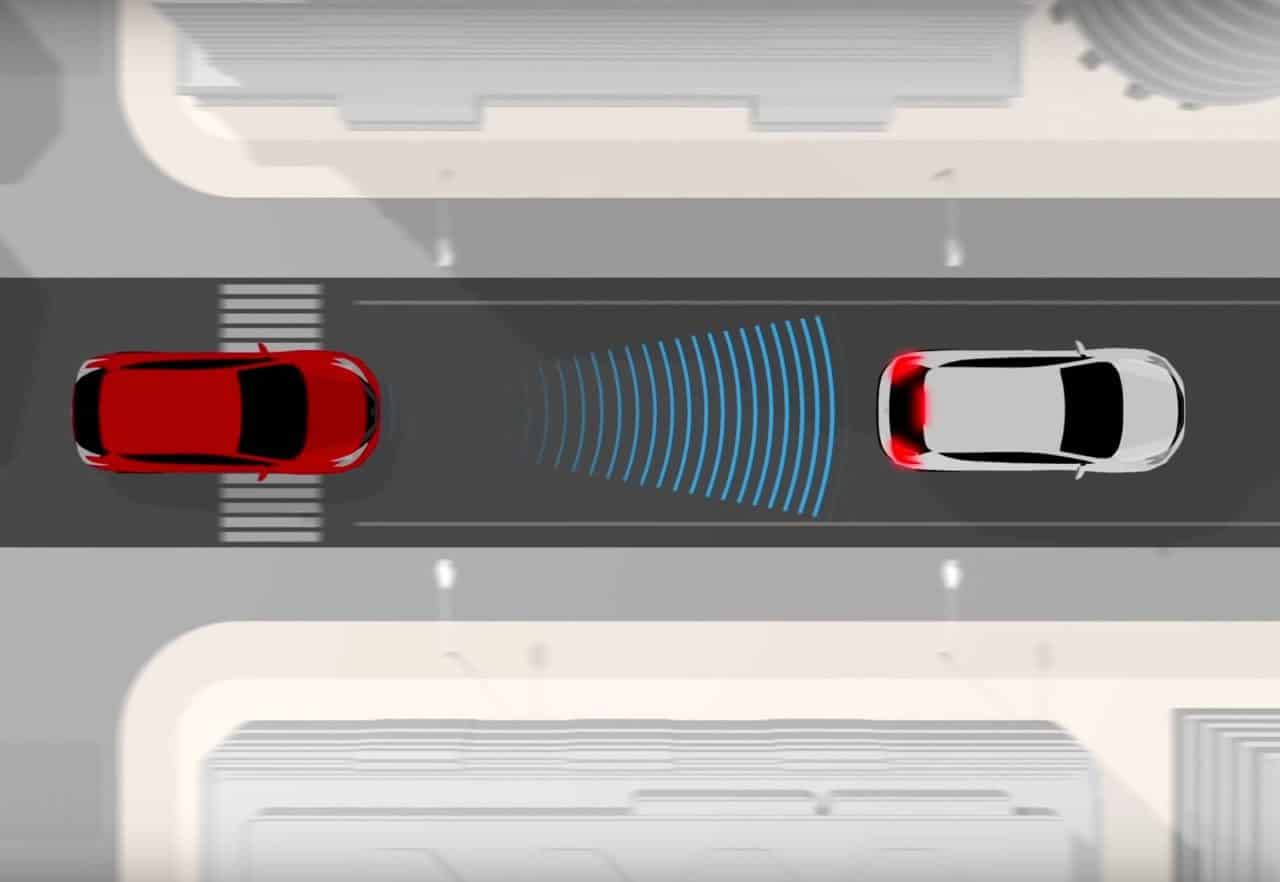
Một xe bán tải khối lượng 2,5 tấn đang di chuyển trên cao tốc với tốc độ 90 km/h. Các xe cần giữ khoảng cách an toàn so với xe chạy phía trước 70 m. Khi xe đi trước có sự cố và dừng lại đột ngột. Để dừng lại an toàn, xe bán tải hãm phanh với một lực cản Fc.

Câu hỏi trong đề: Bài tập ôn tập Vật lí 10 Cánh diều Chủ đề 2 có đáp án !!
Quảng cáo
Trả lời:

a) Gia tốc tối thiểu của xe bán tải \(a = \frac{{({v^2} - {v_0}^2)}}{{2s}} = \frac{{{{25}^2}}}{{2.70}} = 4,46(m/{s^2})\)
b) Khi xe hãm phanh, lực kéo động cơ nhỏ hơn lực hãm phanh.
c) \[t = \frac{{v - {v_0}}}{a} = \frac{{0 - \frac{{90}}{{3,6}}}}{{4,46}} = 5,6s\]
d) Fc = - ma = 11150N
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 10 VietJack - Sách 2025 theo chương trình mới cho 2k9 ( 31.000₫ )
- Trọng tâm Lí, Hóa, Sinh 10 cho cả 3 bộ KNTT, CTST và CD VietJack - Sách 2025 ( 40.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
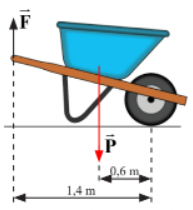
Ta có: Mxuôi = Mngược F. 1,4 = (200.9,8).0,6 F = 840 N.
Lời giải
Gia tốc của ô tô: \(a = \frac{{v - {v_0}}}{{\Delta t}} = \frac{{20 - 10}}{{20}} = 0,5m/{s^2}\)
Vận dụng định luật II Newton:
\({F_k} - {F_{ms}} = ma \to {F_k} = ma + {F_{ms}} = 600.0,5 + 1500N = 1800N\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
2 cm.
3 cm.
3,5 cm.
2,2 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.