(0,5 điểm) Một sợi dây thép \(AC\) có chiều dài \({\rm{8 m}}\)được chia thành hai phần \(AB,\,\,BC\) (như hình vẽ minh họa dưới đây).

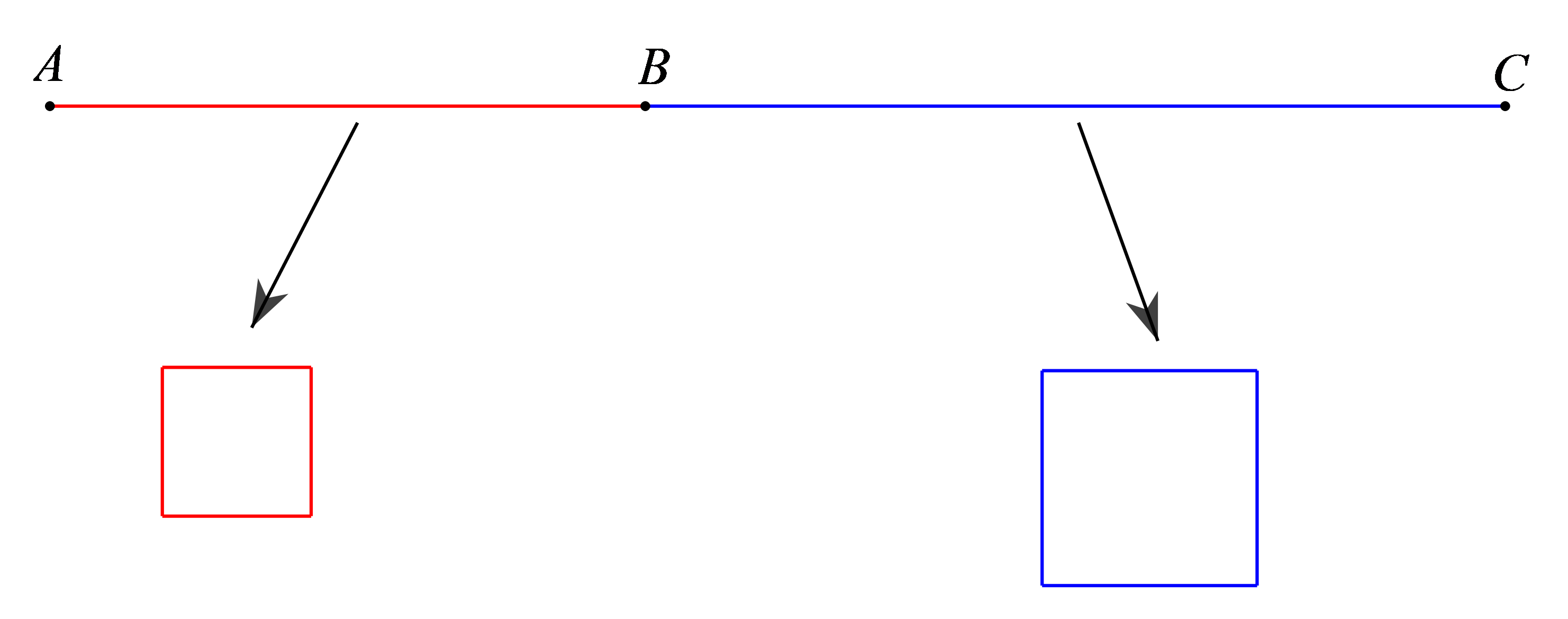
Mỗi phần đều được uốn thành một hình vuông. Hỏi phải chia sợi dây ban đầu như thế nào để tổng diện tích hai hình vuông thu được sau khi uốn là nhỏ nhất?

Hướng dẫn giải

a) Vì \(AM,\,\,AN\) là hai tiếp tuyến của đường tròn \(\left( O \right)\) lần lượt tại \(M,\,\,N\) nên \(AM \bot OM,\,\,AN \bot ON.\)

Gọi \[E\] là trung điểm của \[OA\]. Khi đó \(OE = AE = \frac{1}{2}OA.\)

Xét \[\Delta MOA\] vuông tại \[M\] có \[ME\] là đường trung tuyến ứng với cạnh huyền \(OA\) nên \[ME = \frac{1}{2}OA\].

Xét \[\Delta NOA\] vuông tại \[N\] có \[NE\] là đường trung tuyến ứng với cạnh huyền \(OA\) nên \[NE = \frac{1}{2}OA\].

Vì \[NE = ME = OE = AE = \frac{1}{2}OA\] nên bốn điểm \[A,M,O,N\] cùng thuộc đường tròn tâm \[E,\] đường kính \[OA\].

b) Xét \[\Delta COB\] cân tại \[O\] (do \[OC = OB\]) có \[OI\] là đường trung tuyến nên đồng thời là đường cao, do đó \[OI \bot BC\]. Suy ra \[\Delta IOA\] vuông tại \[I\].

Xét \[\Delta IOA\] vuông tại \[I\] có \[IE\] là đường trung tuyến ứng với cạnh huyền \(OA\) nên \[IE = \frac{1}{2}OA\].

Khi đó, ta có \[NE = IE = OE = AE = \frac{1}{2}OA\] nên bốn điểm \[A,I,O,N\] cùng thuộc đường tròn tâm \[E,\] đường kính \[OA\].

Suy ra \[\widehat {AIN} = \widehat {AON}\] (hai góc nội tiếp cùng chắn cung \[AN\] của đường tròn tâm \[E\]). (*)

Xét đường tròn \(\left( O \right)\) có \[AM,AN\] là hai tiếp tuyến cắt nhau tại \[A\], suy ra \[OA\] là phân giác của \[\widehat {MON}\]

Do đó, \[\widehat {AON} = \frac{1}{2}\widehat {MON}\].

Mà \[\widehat {NFM} = \frac{1}{2}\widehat {MON}\] (góc nội tiếp và góc ở tâm cùng chắn cung \[MN\])

Suy ra \[\widehat {NFM} = \widehat {AON}\] (**)

Từ (*) và (**), suy ra \[\widehat {NFM} = \widehat {AIN}\].

Mà hai góc này ở vị trí đồng vị, do đó \[MF\,{\rm{//}}\,AC\].

c)

⦁ Gọi \(H\) là giao điểm của \(MN\) và \(OA.\)

Ta có \(AM = AN\) (tính chất hai tiếp tuyến cắt nhau) và \(OM = ON\) nên \(A,\,\,O\) cùng nằm trên đường trung trực của \(MN\) hay \(OA\) là đường trung trực của \(MN\).

Suy ra \[MN \bot OA\] hay \[HN \bot OA\].

Xét \[\Delta OHN\] và \[\Delta ONA\], có: \[\widehat {OHN} = \widehat {ONA} = 90^\circ \] và \[\widehat {AON}\] là góc chung

Do đó (g.g)

Suy ra \[\frac{{OH}}{{ON}} = \frac{{ON}}{{OA}}\] suy ra \[OH.OA = O{N^2} = {R^2}\] (3).

⦁ Ta có \(OC = OB,\,\,IC = IB\) (do \(I\) là trung điểm của \(BC),\) \(KC = KB\) (tính chất hai tiếp tuyến cắt nhau) nên ba điểm \(O,\,\,I,\,\,K\) thẳng hàng.

Xét \[\Delta OIB\] và \[\Delta OBK\], có: \[\widehat {OIB} = \widehat {OBK} = 90^\circ \] và \[\widehat {BOK}\] là góc chung

Do đó  (g.g)

Suy ra \[\frac{{OI}}{{OB}} = \frac{{OB}}{{OK}}\] suy ra \[OI.OK = O{B^2} = {R^2}\] (4).

Từ (3) và (4) suy ra \[OI.OK = OH.OA = {R^2}.\] Từ đó, ta có \[\frac{{OI}}{{OH}} = \frac{{OA}}{{OK}}\].

Xét \[\Delta OIA\] và \[\Delta OHK\] có: \[\widehat {AOK}\] là góc chung và \[\frac{{OI}}{{OH}} = \frac{{OA}}{{OK}}\]

Do đó  (c.g.c)

Suy ra \[\widehat {OHK} = \widehat {OIA} = 90^\circ \], suy ra \[HK \bot OA\].

Mà \[MN \bot OA\] tại \[H\] và \[MN\] cố định (do điểm \(A\) cố định), do đó \[K\] thuộc \[MN\] cố định.

Hướng dẫn giải

Đáp án đúng là: C

Ta có: \(\sqrt {{a^2}} = \left| a \right|\), do đó:

Nếu \(\sqrt {{a^2}} = - a\) thì \(a \le 0.\)