Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tìm giá trị của \(x\) thỏa mãn phương trình: \(\frac{{x + 6}}{{x + 5}} + \frac{3}{2} = 2\).
Phần 3. (2,0 điểm) Câu hỏi trắc nghiệm trả lời ngắn
Trong các câu từ 15 đến 18, hãy viết câu trả lời/ đáp án vào bài làm mà không cần trình bày lời giải chi tiết.
Tìm giá trị của \(x\) thỏa mãn phương trình: \(\frac{{x + 6}}{{x + 5}} + \frac{3}{2} = 2\).
Quảng cáo
Trả lời:
Hướng dẫn giải
Đáp án: −7
Điều kiện xác định: \(x \ne - 5\).
Ta có: \(\frac{{x + 6}}{{x + 5}} + \frac{3}{2} = 2\)
\[\frac{{x + 6}}{{x + 5}} = \frac{1}{2}\]
\[2\left( {x + 6} \right) = x + 5\]
\[2x + 12 = x + 5\]
\[2x - x = 5 - 12\]
\[x = - 7\] (thỏa mãn).
Vậy phương trình đã cho có nghiệm \[x = - 7\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Đáp án đúng là: a) Đúng. b) Đúng. c) Sai. d) Đúng.
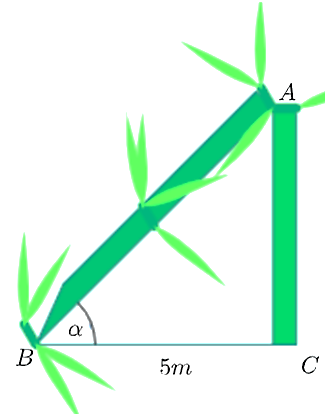
• Theo đề bài, phần ngọn bị gãy \(AB\) và phần gốc \(AC\) có tỉ lệ \(3:2\) hay \(\frac{{AB}}{{AC}} = \frac{3}{2}\), suy ra \(\frac{{AC}}{{AB}} = \frac{2}{3}\).
Xét tam giác \(ABC\) vuông tại \(C\), ta có: \(\sin \widehat {ABC} = \frac{{AC}}{{AB}} = \frac{2}{3}\). Do đó, ý a) là đúng.
• Vì \(\sin \widehat {ABC} = \frac{{AC}}{{AB}} = \frac{2}{3}\) nên \(\alpha = \widehat {ABC} \approx 41^\circ 49'.\) Do đó, ý b) là đúng.
• Xét tam giác \(ABC\) vuông tại \(C\), ta có: \(AC = BC \cdot \tan \widehat {ABC} \approx 5 \cdot \tan 41^\circ 49' \approx 4,47{\rm{\;(m)}}{\rm{.}}\)
Mà \(\frac{{AB}}{{AC}} = \frac{3}{2}\), suy ra \(AB = \frac{3}{2}AC \approx \frac{3}{2} \cdot 4,47 = 6,705{\rm{ (m)}}{\rm{.}}\)
Độ dài phần ngọn bị gãy là độ dài đoạn thẳng \(AB\). Do đó, ý c) là sai.
• Độ dài cây ban đầu là tổng của phần ngọn bị gãy \(AB\) và phần gốc \(AC\).
Vậy chiều cao ban đầu của cây khoảng: \[4,47 + 6,705 = 11,175 \approx 11,18{\rm{\;(m)}}{\rm{.}}\]Do đó, ý d) là đúng.
Lời giải
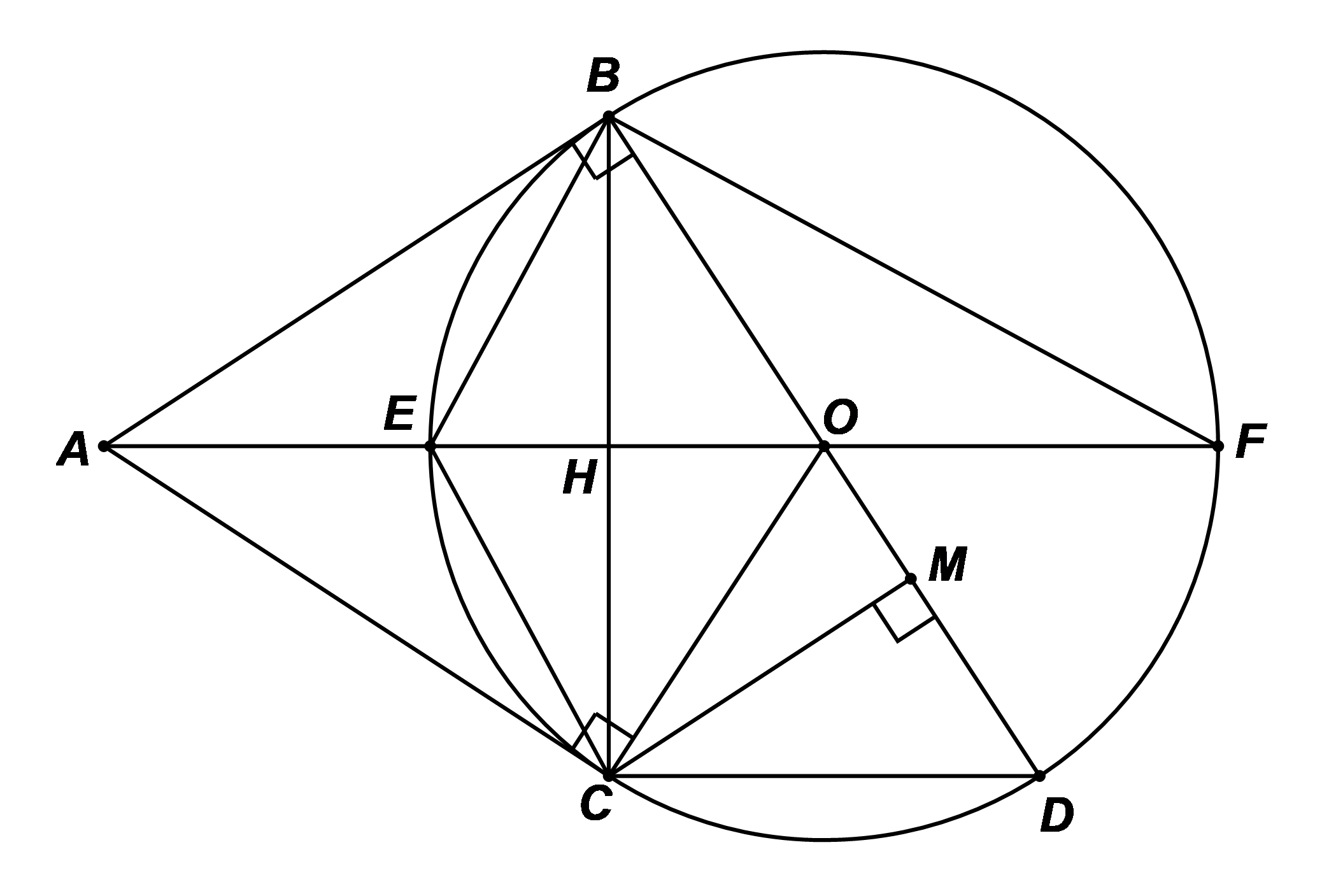
a) Ta có: \(AB,AC\) là hai tiếp tuyến của đường tròn \(\left( O \right)\), suy ra \(OA\) là đường phân giác của \(\widehat {BOC}\) (tính chất) nên \(\widehat {AOC} = \frac{1}{2}\widehat {BOC}.\)
Xét đường tròn \(\left( O \right)\), ta có: \(\widehat {CDB} = \frac{1}{2}\widehat {BOC}\) (góc nội tiếp và góc ở tâm cùng chắn cung \(BC\))
Do đó, \(\widehat {AOC} = \widehat {CDB}\).
Xét \(\Delta CMD\) và \(\Delta ACO\) có:
\(\widehat {CMD} = \widehat {ACO} = 90^\circ \) và \(\widehat {CDM} = \widehat {AOC}\) (do \(\widehat {AOC} = \widehat {CDB}\))
Do đó (g.g).
b) Xét đường tròn \(\left( O \right)\), ta có: \(\widehat {EBF} = 90^\circ \) (góc nội tiếp chắn nửa đường tròn).
Ta có \(\widehat {ABO} = \widehat {EBF} = 90^\circ \) nên \(\widehat {ABE} + \widehat {EBO} = \widehat {EBO} + \widehat {OBF}\)
Suy ra \(\widehat {ABE} = \widehat {OBF}\).
Lại có: \(\widehat {OBF} = \widehat {OFB}\) (vì \(\Delta BOF\) cân tại \(O\) do \(OB = OF)\) suy ra \(\widehat {ABE} = \widehat {OFB}\) (1)
Mà \(\widehat {ECB} = \widehat {OFB}\) (hai góc nội tiếp cùng chắn cung \(EC\) của đường tròn tâm \(O\)) (2)
Từ (1) và (2) suy ra \(\widehat {ECB} = \widehat {ABE}\). (3)
Mặt khác, \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau) và \(OB = OC = R\)
Suy ra \(OA\) là đường trung trực của \(BC\) mà \(E \in OA\), suy ra \(EB = EC\).
Do đó \(\Delta EBC\) cân tại \(E\) nên \(\widehat {ECB} = \widehat {EBC}\). (4)
Từ (3) và (4) suy ra \(\widehat {EBC} = \widehat {ABE}\) nên \(BE\) là tia phân giác của góc \(B\) trong tam giác \(ABH\).
Vậy \[BE\] là phân giác của \(\widehat {ABC}.\)
c) Theo câu a, (g.g), suy ra \(\widehat {OAC} = \widehat {DCM} = 30^\circ \).
Suy ra \(\widehat {AOC} = 90^\circ - \widehat {OAC} = 90^\circ - 30^\circ = 60^\circ \).
Do đó, \(\widehat {BOC} = 2\widehat {AOC} = 120^\circ \) hay
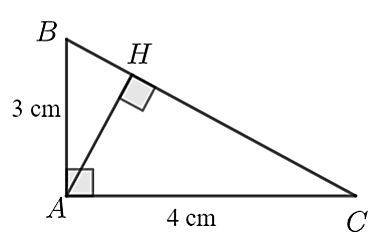
Xét \(\Delta AHC\) vuông tại \(H\), có: \(\cos \widehat {HAC} = \frac{{AH}}{{AC}}\)
Suy ra \(AC = \frac{{AH}}{{\cos \widehat {HAC}}} = \frac{4}{{\cos 30^\circ }} = \frac{{8\sqrt 3 }}{3}{\rm{ }}\left( {{\rm{cm}}} \right).\)
Xét \(\Delta AOC\) vuông tại \(C\), có: \(OC = AC.\tan \widehat {OAC} = \frac{{8\sqrt 3 }}{3}.\tan 30^\circ = \frac{8}{3}{\rm{ }}\left( {{\rm{cm}}} \right).\)
Diện tích hình quạt giới hạn bởi các bán kính \[OB,OC\] và cung nhỏ \(BC\) là:
\[S = \frac{{\pi .{{\left( {\frac{8}{3}} \right)}^2} \cdot 120}}{{360}} = \frac{{64\pi }}{{27}}{\rm{ }}\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(\sqrt {{x^3}} .\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\cot \widehat {CAH} = \frac{3}{4}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Bác An có mảnh vườn hình vuông \[ABCD\] (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/25-1761112465.png)