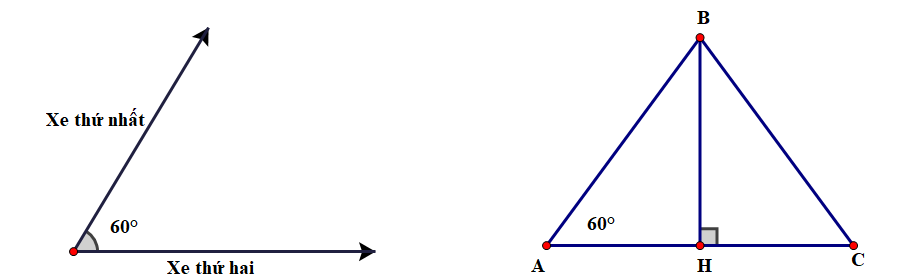
Hai xe máy khởi hành cùng lúc tại A và đi theo hai hướng tạo thành góc \(60^\circ \) (như hình vẽ). Xe thứ nhất đi với vận tốc trung bình \(40\;\,{\rm{km}}/{\rm{h}}\), xe thứ hai đi với vận tốc trung bình \(50\,\;{\rm{km}}/{\rm{h}}\). Hỏi sau khi khởi hành 150 phút, hai xe cách nhau bao nhiêu km? (kết quả làm tròn đến hàng đơn vị)
Câu hỏi trong đề: Bài tập ôn tập Toán 9 Kết nối tri thức Chương 4 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đổi 150 phút \( = \frac{{150}}{{60}} = 2,5\) giờ.
Quãng đường xe thứ nhất đi được sau \[2,5\] giờ là: \(AB = 40 \cdot 2,5 = 100\;\,\,({\rm{km}}).\)
Quãng đường xe thứ hai đi được sau \(2,5\) giờ là: \(AC = 50 \cdot 2,5 = 125\;\,\,({\rm{km}})\).
Xét \(\Delta ABH\) vuông tại \(H\), ta có:
\(\cos A = \frac{{AH}}{{AB}}\) hay \(\cos 60^\circ = \frac{{AH}}{{100}}\) nên \(AH = 100 \cdot \cos 60^\circ = 50\;\,\,({\rm{km)}}\).
Khi đó \(HC = AC - AH = 125 - 50 = 75\,\,({\rm{km}}).\)
\(BH = \sqrt {A{B^2} - A{H^2}} = \sqrt {{{100}^2} - {{50}^2}} \approx 86,6\;\,\,({\rm{km}}).\) (theo định lí Pythagore)
Xét \(\Delta BHC\) vuông tại \(H\), ta có:
\(BC = \sqrt {B{H^2} + H{C^2}} = \sqrt {86,{6^2} + {{75}^2}} \approx 115\;\,\,({\rm{km}})\). (theo định lí Pythagore)
Vậy sau khi khởi hành 150 phút, hai xe cách nhau \(115\;\,{\rm{km}}\).
Đáp án: 115.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Do mặt đất là phương ngang nên \[\widehat {BCA} = 30^\circ \] và \[\widehat {BDA} = 60^\circ \].
Gọi \[x\] (m/phút) là vận tốc xe máy, điều kiện \[x > 0\].
Vì xe máy đi từ \[C\] đến \[D\] trong \[6\] phút nên \[CD = 6x\,\,\left( {\rm{m}} \right)\]
• Xét \[\Delta ABC\] vuông tại \[A\], ta có:
\[AC = AB \cdot \cot \widehat {BCA} = AB \cdot \cot 30^\circ = AB \cdot \tan 60^\circ = \sqrt 3 AB\] (do \[\cot 30^\circ = \tan 60^\circ \]) \[\left( 1 \right)\]
• Xét \[\Delta ABD\] vuông tại \[A\], ta có:
\[AD = AB \cdot \,\cot \widehat {BDA} = AB \cdot \,\cot 60^\circ = AB \cdot \tan 30^\circ = \frac{{\sqrt 3 AB}}{3}\] (do \[\cot 60^\circ = \tan 30^\circ \]) \[\left( 2 \right)\]
Từ \[\left( 1 \right)\] và \[\left( 2 \right)\] suy ra \[AC - AD = AB\left( {\sqrt 3 - \frac{{\sqrt 3 }}{3}} \right)\] nên \[CD = \frac{{2\sqrt 3 }}{3}AB\].
Ta có \[\frac{{AD}}{{CD}} = \frac{{\sqrt 3 AB}}{3}:\frac{{2\sqrt 3 }}{3}AB = \frac{1}{2}\].
Suy ra \[AD = \frac{1}{2}CD = \frac{1}{2} \cdot 6x = 3x\,\,({\rm{m}}).\]
Vậy thời gian để xe máy chạy từ \[D\] đến tòa nhà là \[\frac{{3x}}{x} = 3\] (phút).
Đáp án: 3.
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Chọn C
Gắn dữ kiện của bài toán vào mô hình Toán học như trên hình vẽ.
Gọi \[N\] là hình chiếu của \[M\] lên đoạn \[AH\].
Vì \[MN\] và \[BH\] là các đoạn thẳng nằm trên phương ngang; \[MB\] và \[NH\] nằm trên phương thẳng đứng nên tứ giác \[MBHN\] là hình chữ nhật.
Suy ra \[NH = MB = 1,55\,\,{\rm{m}}\]; \[MN = BH = 13,65\,\,{\rm{m}}\].
Tam giác \[ANM\] vuông tại \[N\] nên \[AN = MN \cdot \tan M.\]
Ta có:\[AH = AN + NH\]suy ra \[AH = MN \cdot \tan M + NH\].
Do đó \[AH = 13,65 \cdot \tan 58^\circ + 1,55 \approx 23,39\,\,({\rm{m}}).\]
Vậy chiều cao của tháp khoảng \[23,39\,\,{\rm{m}}\].
![Từ hai vị trí \[A\] và \[B\] của một tòa nhà, người ta dùng một dụn (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2025/10/38-1761183129.png)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập