Phần III. Trắc nghiệm trả lời ngắn
Cho hình vẽ các tam giác \(ABC,\,ACD,\,\,CDE\) là tam giác đều, \(AC\) bằng \(9{\rm{ cm}}{\rm{.}}\)
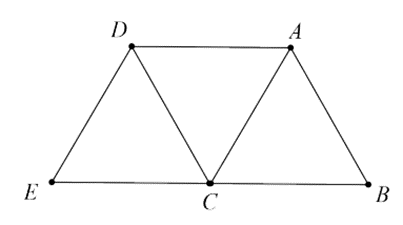
Độ dài cạnh \(DE\) bằng bao nhiêu centimet?
Phần III. Trắc nghiệm trả lời ngắn
Cho hình vẽ các tam giác \(ABC,\,ACD,\,\,CDE\) là tam giác đều, \(AC\) bằng \(9{\rm{ cm}}{\rm{.}}\)

Độ dài cạnh \(DE\) bằng bao nhiêu centimet?
Quảng cáo
Trả lời:
Đáp án: 9
Do các tam giác \(ABC,\,ACD,\,\,CDE\) là các tam giác đều nên ta có: \(AC = DC = DE = 9{\rm{ cm}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án: 18
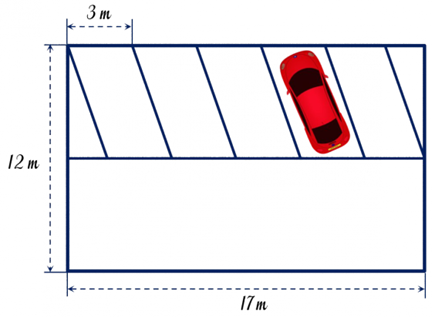
Chiều cao của chỗ đậu xe cho một ô tô là \(12:2 = 6{\rm{ }}\left( {\rm{m}} \right){\rm{.}}\)
Diện tích ô dành cho một xe đậu là: \(3 \cdot 6 = 18{\rm{ }}\left( {{{\rm{m}}^2}} \right){\rm{.}}\)
Lời giải
a) Sai
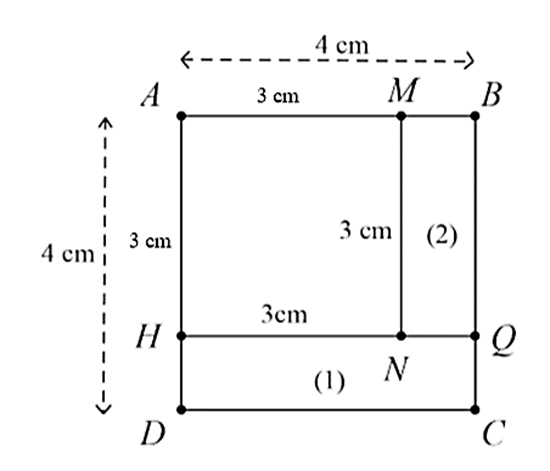
Chu vi một cánh hoa là: \(4 \cdot 4 = 16{\rm{ }}\left( {{\rm{cm}}} \right)\).
b) Sai.
Chu vi một chiếc lá là: \(4 \cdot 3 = 12{\rm{ }}\left( {{\rm{cm}}} \right)\).
Do đó, chu vi một cánh hoa lớn hơn chu vi một chiếc lá.
c) Đúng.
Có tất cả 6 cánh hoa.
Do đó, tổng chu vi giấy màu để làm tất cả cánh hoa cho bông hoa đó là: \(16 \cdot 4 = 64{\rm{ }}\left( {{\rm{cm}}} \right)\).
d) Đúng.
Có hai chiếc lá.
Do đó, tổng chu vi giấy màu để làm lá cho bông hoa đó là: \(12 \cdot 2 = 24{\rm{ }}\left( {{\rm{cm}}} \right)\).
Vậy tổng chu vi giấy màu để làm cánh hoa và lá của bông hoa đó là: \(24 + 64 = 88{\rm{ }}\left( {{\rm{cm}}} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.