Cho hình chóp tam giác đều \(S.ABC\) như hình vẽ:
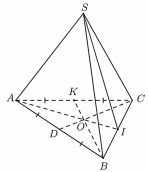
Biết rằng \(AB = 12\;{\rm{cm,}}\;\,SI = \frac{4}{3}AB.\) Khi đó:
( a) \(O\) là trọng tâm của tam giác \(ABC.\)
(b) \(I\) là trung điểm của \(BC.\)
(c) \(SI\) là trung đoạn của hình chóp \(S.ABC.\)
(d) Diện tích xung quanh của hình chóp \(S.ABC\) bằng \(144\;{\rm{c}}{{\rm{m}}^2}.\)
Quảng cáo
Trả lời:
a) Đúng.
Vì \(O\) là giao điểm của hai đường trung tuyến \(BK\) và \(CD\) của tam giác \(ABC\) nên \(O\) là trọng tâm của tam giác \(ABC.\)
b) Đúng.
Vì \(AO\) cắt \(BC\) tại \(I\) và \(O\) là trọng tâm của tam giác \(ABC\) nên \(AI\) là trung tuyến của tam giác \(ABC.\) Do đó, \(I\) là trung điểm của \(BC.\)
c) Đúng.
Vì \(S.ABC\) là hình chóp tam giác đều nên tam giác \(SBC\) cân tại \(S.\) Do đó, \(SI\) là đường trung tuyến đồng thời là đường cao của tam giác \(SBC.\) Do đó, \(SI\) là trung đoạn của hình chóp \(S.ABC.\)
d) Sai.
Ta có: \(SI = \frac{4}{3} \cdot 12 = 16\;\,\left( {{\rm{cm}}} \right).\)
Diện tích xung quanh của hình chóp \(S.ABC\) là: \(\frac{1}{2}\left( {12 + 12 + 12} \right) \cdot 16 = 288\;\,\left( {{\rm{c}}{{\rm{m}}^2}} \right).\)
Vậy diện tích xung quanh của hình chóp \(S.ABC\) bằng \(288\;\,{\rm{c}}{{\rm{m}}^2}.\)
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
\(SO.\)
\(OA.\)
\(CO.\)
\(BO.\)
Lời giải
Đáp án đúng là: A
Đoạn thẳng nối đỉnh của hình chóp và trọng tâm của tam giác đáy gọi là đường cao của hình chóp tam giác đều.
Vì \(O\) là trọng tâm của tam giác \(ABC\) nên \(SO\) là đường cao của hình chóp \(S.ABC.\)
Câu 2
3 cạnh.
4 cạnh.
5 cạnh.
6 cạnh.
Lời giải
Đáp án đúng là: A
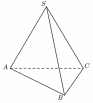
Hình chóp tam giác đều \(S.ABC\) có tất cả 3 cạnh bên là: \(SA;\;\,SB;\;\,SC.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
\(120\;{\rm{c}}{{\rm{m}}^2}.\)
\(120\;{\rm{c}}{{\rm{m}}^3}.\)
\(40\;{\rm{c}}{{\rm{m}}^3}.\)
\(40\;{\rm{c}}{{\rm{m}}^2}.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Hình 1
Hình 2.
Hình 3.
Hình 4.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Hình vuông.
Hình tam giác đều.
Hình tam giác vuông.
Hình chữ nhật.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.