Một cửa hàng trang sức khảo sát khách hàng xem họ dự định mua trang sức với mức giá nào (đơn vị: triệu đồng). Kết quả khảo sát được ghi lại ở bảng sau:
Mức giá
\([6;9)\)
\([9;12)\)
\([12;15)\)
\([15;18)\)
\([18;21)\)
Số khác hàng
20
78
45
23
12
a) Tìm khoảng biến thiên của mẫu số liệu ghép nhóm.
b) Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn đến hai chữ số thập phân).
Một cửa hàng trang sức khảo sát khách hàng xem họ dự định mua trang sức với mức giá nào (đơn vị: triệu đồng). Kết quả khảo sát được ghi lại ở bảng sau:
|
Mức giá |
\([6;9)\) |
\([9;12)\) |
\([12;15)\) |
\([15;18)\) |
\([18;21)\) |
|
Số khác hàng |
20 |
78 |
45 |
23 |
12 |
a) Tìm khoảng biến thiên của mẫu số liệu ghép nhóm.
b) Tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn đến hai chữ số thập phân).
Quảng cáo
Trả lời:
a) Khoảng biến thiên của mẫu số liệu ghép nhóm là \(R = 21 - 6 = 15\).
b) Ta có bảng tần số tích lũy
|
Nhóm |
Tần số |
Tần số tích lũy |
|
\([6;9)\) |
20 |
20 |
|
\([9;12)\) |
78 |
98 |
|
\([12;15)\) |
45 |
143 |
|
\([15;18)\) |
23 |
166 |
|
\([18;21)\) |
12 |
178 |
Nhóm 2 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{n}{4} = \frac{{178}}{4} = 44,5\)
\( \Rightarrow {Q_1} = 9 + \left( {\frac{{44,5 - 20}}{{78}}} \right).3 = \frac{{517}}{{52}}\).
Nhóm 3 là nhóm đầu tiên có tần số tích lũy lớn hơn hoặc bằng \(\frac{{3n}}{4} = \frac{{3.178}}{4} = 133,5\)
\( \Rightarrow {Q_3} = 12 + \left( {\frac{{133,5 - 98}}{{45}}} \right).3 = \frac{{431}}{{30}}\).
Khoảng tứ phân vị: \({\Delta _Q} = Q{}_3 - {Q_1} = \frac{{431}}{{30}} - \frac{{517}}{{52}} = \frac{{3451}}{{780}} \approx 4,42\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- 500 Bài tập tổng ôn môn Toán (Form 2025) ( 38.500₫ )
- 20 đề thi tốt nghiệp môn Toán (có đáp án chi tiết) ( 38.500₫ )
- Sổ tay lớp 12 các môn Toán, Lí, Hóa, Văn, Sử, Địa, KTPL (chương trình mới) ( 36.000₫ )
- Tuyển tập 30 đề thi đánh giá năng lực Đại học Quốc gia Hà Nội, TP Hồ Chí Minh (2 cuốn) ( 150.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
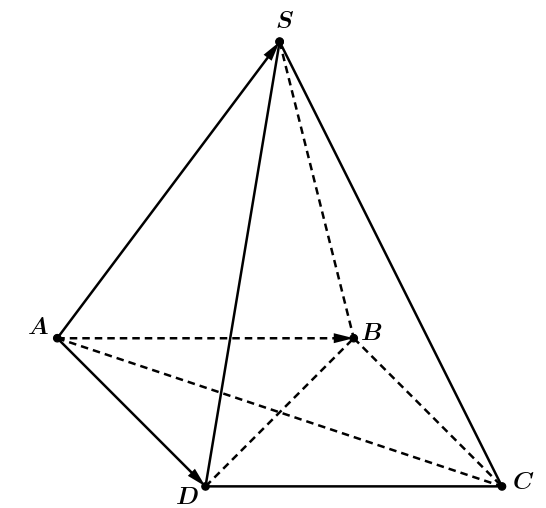
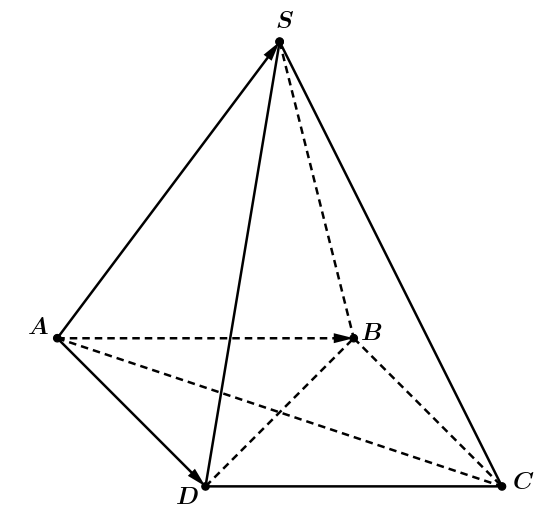
Ta có \[\overrightarrow {AB} = \left( {3;\,\,0;\,\,0} \right)\]. Gọi \(C\left( {x;\,y;\,\,z} \right) \Rightarrow \overrightarrow {DC} = \left( {x;\,\,y - 3;\,\,z} \right)\).
\(ABCD\) là hình bình hành \[ \Rightarrow \overrightarrow {AB} = \overrightarrow {DC} \Rightarrow \left( {x;\,\,y - 3;\,\,z} \right) = \left( {3;\,\,0;\,\,0} \right) \Rightarrow C\left( {3;\,\,3;\,\,0} \right)\]
Ta có \(\overrightarrow {AD} = \left( {0;\,\,3;\,\,0} \right)\). Gọi \(A'\left( {x';\,\,y';\,\,z'} \right) \Rightarrow \overrightarrow {A'D'} = \left( { - x';\,\,3 - y';\,\, - 3 - z'} \right)\)
\(ADD'A'\) là hình bình hành \( \Rightarrow \overrightarrow {AD} = \overrightarrow {A'D'} \Rightarrow \left( {x';\,\,y';\,\,z'} \right) = \left( {0;\,\,0;\,\, - 3} \right) \Rightarrow A'\left( {0;\,\,0;\, - 3} \right)\).
Gọi \(B'\left( {{x_0};\,\,{y_0};\,\,{z_0}} \right) \Rightarrow \overrightarrow {A'B'} = \left( {{x_0};\,\,{y_0};\,\,{z_0} + 3} \right)\)
\(ABB'A'\) là hình bình hành \( \Rightarrow \overrightarrow {AB} = \overrightarrow {A'B'} \Rightarrow \left( {{x_0};\,\,{y_0};\,\,{z_0}} \right) = \left( {3;\,\,0;\, - 3} \right) \Rightarrow B'\left( {3;\,\,0;\, - 3} \right)\)
\(G\) là trọng tâm tam giác \(A'B'C\) \[ \Rightarrow \left\{ \begin{array}{l}{x_G} = \frac{{0 + 3 + 3}}{3} = 2\\{y_G} = \frac{{0 + 0 + 3}}{3} = 1\\{z_G} = \frac{{ - 3 - 3 + 0}}{3} = - 2\end{array} \right. \Rightarrow G\left( {2;\,\,1;\,\, - 2} \right)\].
Lời giải
Số cá giống mà ông thanh đã thả trong vụ vừa qua là \(50.20 = 1000\left( {{\rm{con}}} \right)\)
Khối lượng trung bình mỗi con cá thành phần trong vụ vừa qua là: \(1500:1000 = 1,5\left( {{\rm{kg}}} \right)\).
Gọi số cá giống cần thả ít đi trong vụ này là: \(x\left( {{\rm{con}}} \right),\left( {x > 0} \right)\)
Theo đề, giảm 8 con thì mỗi con tăng thêm \(0,5\;{\rm{kg/con}}\)
Vậy giảm \(x\) con thì mỗi con tăng thêm \(0,0625x{\rm{ kg/con}}\).
Tổng số lượng cá thu được ở vụ này:
\(F\left( x \right) = \left( {1000 - x} \right)\left( {1,5 + 0,0625x} \right) = - 0,0625{x^2} + 61x + 1500\).
Bài toán trở thành tìm x để \(F\left( x \right)\) đạt giá trị lớn nhất.
Ta có:\(F'\left( x \right) = - 0,125x + 61\)
\(F'\left( x \right) = 0 \Leftrightarrow - 0,125x + 61 = 0 \Leftrightarrow x = 488\)
Bảng biến thiên
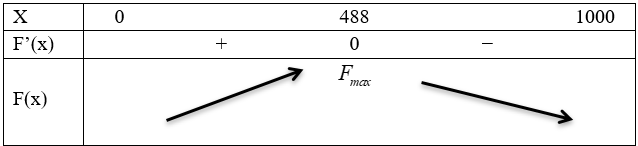
Vậy ông thanh phải thả số cá giống trong vụ này là: \(1000 - 488 = 512\;{\rm{con}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.