Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình bình hành tâm \[O\], \[I\] là trung điểm cạnh \[SC\]. Xét các mệnh đề:
(I). Đường thẳng \[IO\] song song \[SA\].
(II). Mặt phẳng \[\left( {IBD} \right)\] cắt hình chóp \[S.ABCD\] theo thiết diện là một tứ giác.
(III). Giao điểm của đường thẳng \[AI\] và mặt phẳng \[\left( {SBD} \right)\] là trọng tâm tam giác \[SBD\].
(IV). Giao tuyến hai mặt phẳng \[\left( {IBD} \right)\] và \[\left( {SAC} \right)\] là \[OI\].
Số mệnh đề đúng trong các mệnh đề trên là:
Câu hỏi trong đề: Bộ 19 đề thi Giữa kì 1 Toán 11 có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Chọn D
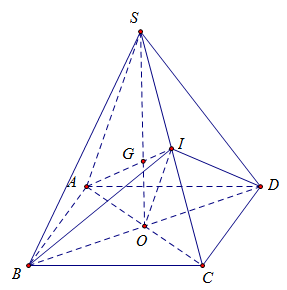
\[IO\] là đường trung bình trong tam giác \[SAC\] nên \[IO{\rm{ //}}\;SA\], do đó mệnh đề (I) đúng.
Mặt phẳng \[IBD\] cắt hình chóp the thiết diện là tam giác \[IBD\], do đó mệnh đề (II) sai.
\[AI \cap SO = G\] vậy \[G\] là trọng tâm tam giác \[SAC\] nên \[SG = \frac{2}{3}SO\].
Ta thấy \[SO \subset \left( {SBD} \right)\] nên \[IA \cap \left( {SBD} \right) = G\], \[SO\] là đường trung tuyến nên \[G\] là trọng tâm tam giác \[SBD\]. Vậy mệnh đề (III) đúng.
\[I\] là điểm chung của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {IBD} \right)\].
\[AC \cap BD = O\] nên \[O\] là điểm chung của hai mặt phẳng \[\left( {SAC} \right)\] và \[\left( {IBD} \right)\].
\[\left( {IBD} \right) \cap \left( {SAC} \right) = OI\]. Vậy mệnh đề (IV) đúng.
Vậy có \[3\] mệnh đề đúng.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Sau 3 năm làm việc có 12 quý.
Lương anh Bình nhận được trong quý 1 là \({u_1} = 6.3 = 18\) (triệu đồng)
Lương anh Bình nhận được trong quý 2 là \({u_2} = {u_1} + {u_1}.5\% = {u_1}.1,05\)
Lương anh Bình nhận được trong quý 3 là \({u_3} = {u_2} + {u_2}.5\% = {u_2}.1,05\)
Lập luận tương tự như vậy thì lương anh Bình nhận được trong quý 12 là \({u_{12}} = {u_{11}}.1,05\).
Như vậy, Lương anh Bình nhận được từ quý 1 đến quý 12 là \({u_1},\,{u_2},\,...,{u_{12}}\) lập thành một cấp số nhân có số hạng đầu \({u_1} = 18\) và công bội \(q = 1,05\).
Do đó tổng lương mà anh Bình nhận được sau 3 năm làm việc là \({S_{12}} = {u_1} + {u_2} + ... + {u_{12}} = 18.\left( {\frac{{1 - 1,{{05}^{12}}}}{{1 - 1,05}}} \right) \approx 286,5\) (triệu đồng).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
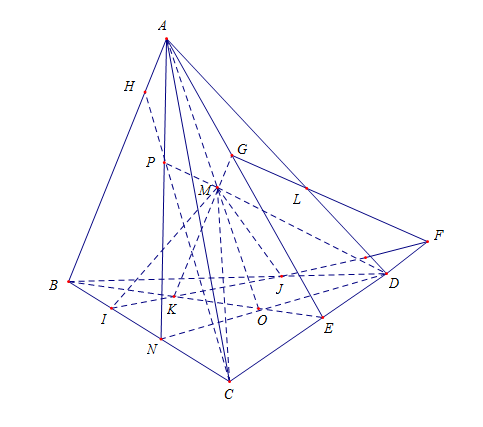
Trong \[\left( {BCD} \right)\] gọi \[E = BO \cap CD,F = IJ \cap CD\], \[K = BE \cap IJ\];
Trong \[\left( {ABE} \right)\] gọi \[G = KM \cap AE\].
Có \[\left\{ \begin{array}{l}F \in IJ \subset \left( {IJM} \right)\\F \in CD \subset \left( {ACD} \right)\end{array} \right. \Rightarrow F \in \left( {IJM} \right) \cap \left( {ACD} \right)\], \[\left\{ \begin{array}{l}G \in KM \subset \left( {IJM} \right)\\G \in AE \subset \left( {ACD} \right)\end{array} \right.\]
\( \Rightarrow (IJM) \cap (ACD) = FG\)
Trong (ACD) gọi \(L = GF \cap AD\). Vậy \(L = AD \cap ({\rm{IJM}}).\)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập