(2,0 điểm) Cho hình vẽ biết \(xx' \bot tt'\), \[yy' \bot tt'\], \(\widehat {zCx'} = 110^\circ \), \(\widehat {CAO} = 50^\circ \), \(\widehat {OBy'} = 140^\circ \).
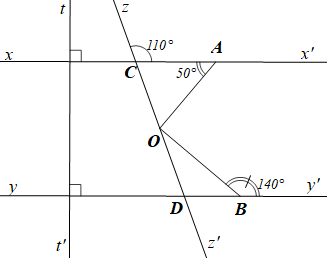
(a) Vẽ lại hình (đúng số đo của các góc) và viết giả thiết, kết luận của bài toán.
(b) Giải thích tại sao \(xx'\,{\rm{//}}\,yy'\).
(c) Tìm số đo của \(\widehat {CDy}\).
(d) Tìm số đo của \(\widehat {AOB}\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Học sinh vẽ lại hình theo đúng số đo các góc.
b) Ta có \(xx' \bot tt'\), \[yy' \bot tt'\] suy ra \(xx'\,{\rm{//}}\,yy'\) (cùng vuông góc với \(tt'\)).
c) Ta có \(\widehat {ACD} + \widehat {zCA} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {ACD} = 180^\circ - \widehat {zCA} = 180^\circ - 110^\circ = 70^\circ \)
Do \(xx'\,{\rm{//}}\,yy'\) (câu b) nên \(\widehat {CDy} = \widehat {ACD} = 70^\circ \) (so le trong)
d) Kẻ \(mn\,{\rm{//}}\,xx'\).
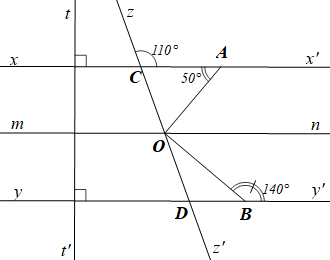
Khi đó \(\widehat {AOn} = \widehat {CAO} = 50^\circ \) (so le trong).
Ta có \(\widehat {DBO} + \widehat {OBy'} = 180^\circ \) (hai góc kề bù)
Suy ra \(\widehat {DBO} = 180^\circ - \widehat {OBy'} = 180^\circ - 140^\circ = 40^\circ \)
Lại có \(xx'\,{\rm{//}}\,yy'\) (câu b) nên \(mn\,{\rm{//}}\,yy'\) (cùng song song với \(xx'\)).
Khi đó \(\widehat {BOn} = \widehat {DBO} = 40^\circ \) (so le trong)
Do đó \[\widehat {AOB} = \widehat {AOn} + \widehat {BOn} = 50^\circ + 40^\circ = 90^\circ \].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
a) Nếu gửi ở ngân hàng \[A\] thì
Tiền lãi sau 1 năm của người đó là: \[150.7\% = {\rm{10,5}}\] (triệu đồng)
Sau 1 năm người đó nhận về số tiền là: \[150 + 10,5 = {\rm{160,5}}\] (triệu đồng)
b) Nếu gửi ở ngân hàng \[B\] thì
Tiền lãi sau 1 năm của người đó là: \[150.6\% = {\rm{9}}\] (triệu đồng)
Sau 1 năm người đó nhận về số tiền là: \[150 + {\rm{9}} + 2 = {\rm{161}}\] (triệu đồng)
Vậy người đó nên gửi ở ngân hàng \[B\] để sau 1 năm có số tiền nhận về nhiều hơn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Câu 3
\(a\,{\rm{//}}\,c\) vì cùng vuông góc với \(b\)
\(a\,{\rm{//}}\,c\) vì cùng song song với \(b\)
\(d \bot b\) vì \(d \bot a\) và \(a\,{\rm{//}}\,b\)
\(d \bot c\) vì \(d \bot b\) và \(b\,{\rm{//}}\,c\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
\(\frac{{ - 4}}{5}\)
\(\frac{{ - 5}}{4}\)
\(\frac{{ - 6}}{5}\)
\(\frac{{ - 1}}{5}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập