Tại cửa hàng điện tử, trong tuần lễ mừng ngày khai trường 05/09, học sinh và sinh viên khi mua một chiếc máy tính sẽ được giảm giá 10% của giá niêm yết và nếu khách hàng mua hàng trực tuyến (giao hàng miễn phí) thì được giảm thêm 5% của giá niêm yết. Chị Phương (là sinh viên một trường đại học) phải trả 12 750 000 đồng khi mua hàng trực tuyến chiếc máy tính đó trong tuần lễ mừng ngày khai trường. Giá niêm yết của chiếc máy tính đó là bao nhiêu?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Chị Phương mua chiếc máy tính đó với giá đã được giảm số phần trăm là:
\(10\% + 5\% = 15\% \).
Giá của chiếc máy tính đó là:
\(12\,\,750\,\,000:\left( {100\% - 15\% } \right) = 15\,\,000\,\,000\) (đồng).
Vậy giá niêm yết của chiếc máy tính đó là \(15\,\,000\,\,000\) đồng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Trọng tâm Toán, Anh, KHTN lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn, Sử, Địa, GDCD lớp 7 (chương trình mới) ( 60.000₫ )
- Trọng tâm Văn - Sử - Địa - GDCD và Toán - Anh - KHTN lớp 7 (chương trình mới) ( 120.000₫ )
- Trọng tâm Toán - Văn - Anh, Toán - Anh - KHTN lớp 6 (chương trình mới) ( 126.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2
\(2,5471...\)
\(6,32\)
\(4,2(15)\)
\(\sqrt 6 \).
Lời giải
Đáp án đúng là: C
• Số \(2,5471...\) là số thập phân vô hạn không tuần hoàn;
• Số \(6,32\) là số thập phân hữu hạn;
• Số \(4,2(15)\) là số thập phân vô hạn tuần hoàn với chu kì 15.
• Số \(\sqrt 6 = 2,4494...\) là số vô tỉ hay là số thập phân vô hạn không tuần hoàn.
Do đó chọn đáp án C.
Câu 3
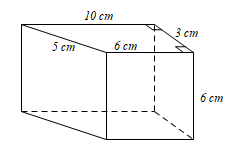
104 cm3
80 cm2
96 cm2
104 cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
\(\frac{6}{0}\)
\( - 2\frac{1}{3}\)
2,75
\(\frac{6}{{11}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.


 ;
; ;
;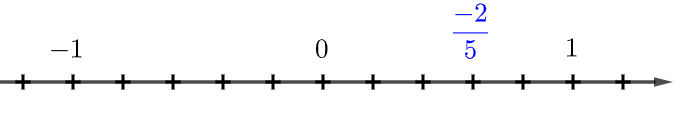 ;
; .
.