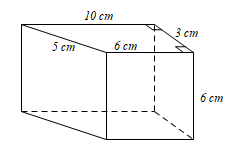
(a) Cho hình lăng trụ đứng có đáy là hình thang vuông với kích thước như hình vẽ.
Tính diện tích xung quanh và thể tích của hình lăng trụ đứng đó.
(b) Một bể bơi có dạng hình hộp chữ nhật với chiều dài là \(12\,\,{\rm{m}}\), chiều rộng là \(5\,\,{\rm{m}}\), chiều sâu là \(1,75\,\,{\rm{m}}\). Người thợ phải dùng bao nhiêu viên gạch men để lát đáy và xung quanh bể đó? Biết rằng mỗi viên gạch có dạng hình chữ nhật với chiều dài là \(25\,\,{\rm{cm}}\), chiều rộng là \(20\,\,{\rm{cm}}\) và diện tích mạch vữa không đáng kể.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
;
;
.Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: B
Cách biểu diễn số \(\frac{{ - 2}}{5}\) trên trục số:
Đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) được chia thành 5 phần bằng nhau, lấy một đoạn làm đơn vị mới thì đơn vị mới bằng \(\frac{1}{5}\) đơn vị cũ.
Điểm biểu diễn số \(\frac{{ - 2}}{5}\) nằm bên trái điểm 0 và cách điểm 0 một đoạn bằng 2 đơn vị mới.
Vậy ta biểu diễn số \(\frac{{ - 2}}{5}\) trên trục số như sau:
Câu 2
\(2,5471...\)
\(6,32\)
\(4,2(15)\)
\(\sqrt 6 \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: C
• Số \(2,5471...\) là số thập phân vô hạn không tuần hoàn;
• Số \(6,32\) là số thập phân hữu hạn;
• Số \(4,2(15)\) là số thập phân vô hạn tuần hoàn với chu kì 15.
• Số \(\sqrt 6 = 2,4494...\) là số vô tỉ hay là số thập phân vô hạn không tuần hoàn.
Do đó chọn đáp án C.
Câu 3
\(\frac{1}{{27}}\)
\(27\)
\(\frac{1}{9}\)
\(9\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
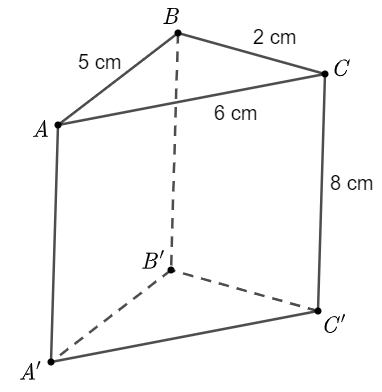
Câu 6
104 cm3
80 cm2
96 cm2
104 cm2.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập