Viết kết quả phép tính \({\left[ {{{\left( { - \frac{2}{3}} \right)}^2}} \right]^6}\) với \(a = - \frac{2}{3}\) dưới dạng lũy thừa của \(a\) ta được
\({a^3}\)
\({a^4}\)
\({a^8}\)
\({a^{12}}\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: D
Ta có \({\left[ {{{\left( { - \frac{2}{3}} \right)}^2}} \right]^6} = {\left( { - \frac{2}{3}} \right)^{2.6}} = {\left( { - \frac{2}{3}} \right)^{12}} = {a^{12}}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
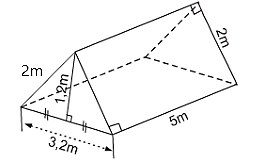
Diện tích xung quanh của lều tại là:
\({S_{xq}} = \left( {2 + 2 + 3,2} \right)\,\,.\,\,5 = 36\) (m2)
Diện tích đáy là:
\({S_d} = 2.\frac{1}{2}\,\,.\,\,1,2\,\,.\,\,3,2 = 3,84\)(m2)
Diện tích vải cần mua để dựng lều là:
\(36 + 3,84 = 39,84\)(m2)
Số tiền cần để mua vải là:
\(39,84\,\,.\,\,150{\rm{ }}000 = 5{\rm{ }}976{\rm{ }}000\) (đồng)
Vì \(6{\rm{ 000 000 > 5 976 000}}\) nên nhóm học sinh đủ tiền mua vải.
Lời giải
Đáp án đúng là: D
Hai số đối nhau có tổng bằng 0.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
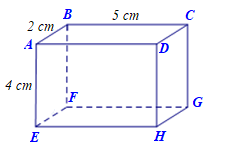
Câu 6
\[CD = 2{\rm{ cm}}\]
\(HG = 4\,\,{\rm{cm}}\)
\(GF = 5\,\,{\rm{cm}}\)
\(DH = 4\,\,{\rm{cm}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.