1. Thực hiệp phép tính (hợp lí nếu có thể)
(a) \(\frac{{ - 5}}{{17}}.\frac{{31}}{{33}} + \frac{{ - 5}}{{17}}.\frac{2}{{33}} + 2\frac{5}{{17}}\)
(b) \(15.{\left( {\frac{2}{3}} \right)^2} + {\left( {\frac{{23}}{6}} \right)^0}.\frac{{24}}{{16}} - 2\frac{2}{3}\).
2. Tìm \(x\), biết:
(a) \(\left( {\frac{1}{2}x - \frac{1}{5}} \right).\frac{{ - 1}}{2} = \frac{3}{4}\)
(b) \(\left| {x + \frac{5}{6}} \right| + \frac{7}{2} = 5\).
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
1.
a) \(\frac{{ - 5}}{{17}}.\frac{{31}}{{33}} + \frac{{ - 5}}{{17}}.\frac{2}{{33}} + 2\frac{5}{{17}}\) \( = \frac{{ - 5}}{{17}}.\left( {\frac{{31}}{{33}} + \frac{2}{{33}}} \right) + 2\frac{5}{{17}}\)
\( = \frac{{ - 5}}{{17}} + 2\frac{5}{{17}}\)\( = 2\);
b) \(15.{\left( {\frac{2}{3}} \right)^2} + {\left( {\frac{{23}}{6}} \right)^0}.\frac{{24}}{{16}} - 2\frac{2}{3}\)
\( = 15.\frac{4}{9} + 1.\frac{{24}}{{16}} - 2\frac{2}{3}\)\( = \frac{{20}}{3} + \frac{3}{2} - \frac{8}{3}\)
\( = \left( {\frac{{20}}{3} - \frac{8}{3}} \right) + \frac{3}{2}\)\( = \frac{{12}}{3} + \frac{3}{2}\)\( = \frac{{11}}{2}\).
2.
a) \(\left( {\frac{1}{2}x - \frac{1}{5}} \right).\frac{{ - 1}}{2} = \frac{3}{4}\)
\(\frac{1}{2}x - \frac{1}{5} = \frac{3}{4}:\frac{{ - 1}}{2}\)
\(\frac{1}{2}x - \frac{1}{5} = \frac{{ - 3}}{2}\)
\(\frac{1}{2}x = \frac{{ - 3}}{2} + \frac{1}{5}\)
\(\frac{1}{2}x = \frac{{ - 13}}{{10}}\)
\(x = \frac{{ - 13}}{{10}}:\frac{1}{2}\)
\(x = \frac{{ - 13}}{5}\)
Vậy \(x = \frac{{ - 13}}{5}\).
b) \(\left| {x + \frac{5}{6}} \right| + \frac{7}{2} = 5\)
\(\left| {x + \frac{5}{6}} \right| = 5 - \frac{7}{2}\)
\(\left| {x + \frac{5}{6}} \right| = \frac{3}{2}\)
Trường hợp 1: \(x + \frac{5}{6} = \frac{3}{2}\)
\(x = \frac{3}{2} - \frac{5}{6}\)
\(x = \frac{2}{3}\)
Trường hợp 2: \(x + \frac{5}{6} = \frac{{ - 3}}{2}\)
\(x = \frac{{ - 3}}{2} - \frac{5}{6}\)
\(x = \frac{{ - 7}}{3}\)
Vậy \(x = \frac{2}{3}\) hoặc \(x = \frac{{ - 7}}{3}\).
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
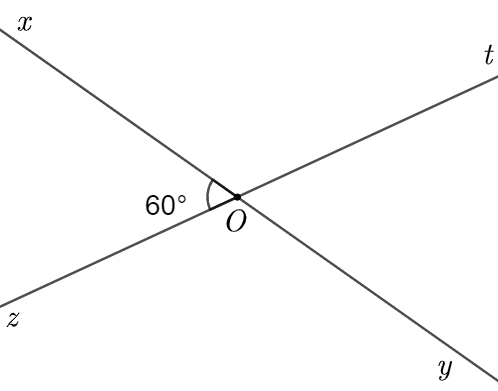
a) Các cặp góc đối đỉnh trong hình là: \(\widehat {xOz}\) và \(\widehat {tOy}\); \(\widehat {xOt}\) và \(\widehat {tOy}\).
b) Từ hình vẽ ta thấy \(\widehat {xOz} = 60^\circ \)
Vì \(\widehat {xOz}\) và \(\widehat {tOy}\) là hai góc đối đỉnh nên \(\widehat {xOz} = \widehat {tOy} = 60^\circ \).
Vì góc \(\widehat {xOz}\)và \(\widehat {xOt}\) là hai góc kề bù nên \(\widehat {xOz} + \widehat {xOt} = 180^\circ \).
Suy ra \(\widehat {xOt} = 180^\circ - \widehat {xOz} = 180^\circ - 60^\circ = 120^\circ \).
Do đó \(\widehat {xOt} = 120^\circ \).
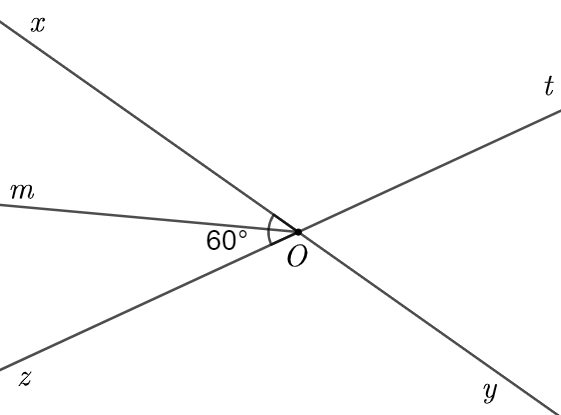
Vì \(Om\) là tia phân giác của \(\widehat {xOz}\) nên \(\widehat {mOx} = \widehat {mOz} = \frac{{\widehat {xOz}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \).
Vậy \(\widehat {tOy} = 60^\circ ;\,\,\widehat {xOt} = 120^\circ ;\,\,\widehat {mOx} = 30^\circ \).
Lời giải
Đáp án đúng là: D
Từ trên xuống ta thấy: Tầng số 1 có 1 hình lập phương; tầng số 2 có 3 hình lập phương; tầng số 3 có 5 hình lập phương.
Số hình lập phương của cả ba tầng là: 1 + 3 + 5 = 9 (hình).
Vậy tổng cả ba tầng có 9 hình lập phương.
Câu 3
30 cm3
15 cm3
30 cm2
15 cm2.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập