Quan sát hình vẽ bên và chọn khẳng định sai:
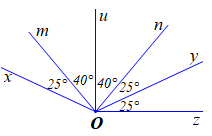
Tia \[Ou\] là tia phân giác của \[\widehat {mOn}\,\]
Tia \[Ou\] là tia phân giác của \[\widehat {xOy}\,\]
Tia \[Oy\] là tia phân giác của \[\widehat {nOz}\,\]
Tia \[On\] là tia phân giác của \[\widehat {mOz}\,\].
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 7 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: D
Ta có \(\widehat {mOn} = 40^\circ + 40^\circ = 80^\circ \) và \(\widehat {nOz} = 25^\circ + 25^\circ = 50^\circ \)
Do đó \(\widehat {mOn} \ne \widehat {nOz}\) nên tia \[On\] không là tia phân giác của \[\widehat {mOz}\,\].
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Chu vi của mặt đáy là: \(2.\left( {3 + 6} \right) = 18\,\,\left( {{\rm{cm}}} \right)\)
Diện tích xung quanh của hình lăng trụ là: \[{S_{xq}} = 18.5 = 90\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{2}}}} \right)\]
Diện tích của mặt đáy là:
Thể tích của hình lăng trụ là: \[V = 12.5 = 60\,\,\left( {{\rm{c}}{{\rm{m}}^{\rm{3}}}} \right)\].
Lời giải
Số tiền chị Hương trả góp trong vòng một năm (12 tháng) là:
\(700.12 = 8\,\,400\) (nghìn đồng) = 8,4 triệu đồng.
Số tiền trả góp này ứng với \(100\% - 40\% = 60\% \) tổng số tiền.
Chị Hương đã mua chiếc điện thoại với số tiền là: \(8,4:60\% = 14\) (triệu đồng).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
\( - \frac{3}{2};\frac{0}{7};\frac{7}{0};\frac{{ - 2}}{{ - 5}}\)
\(1\frac{2}{7};\frac{0}{7};\frac{7}{0};\frac{{ - 2}}{{ - 5}}\)
\( - \frac{3}{2};1\frac{2}{7};\frac{7}{0};\frac{{ - 2}}{{ - 5}}\)
\( - \frac{3}{2};1\frac{2}{7};\frac{0}{7};\frac{{ - 2}}{{ - 5}}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Có 2 đường chéo
Có các mặt bên là hình chữ nhật bằng nhau
Có 6 mặt, 8 cạnh và 12 đỉnh
Có các cạnh bằng nhau.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
\( - \frac{4}{9}\)
\[ - \frac{2}{9}\]
\[\frac{2}{9}\]
\[\frac{4}{9}\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.