Cho \(\Delta ABC\) vuông tại \(A.\) Lấy hai điểm \(M,\;\,N\) lần lượt thuộc các cạnh \(AB,\;\,AC\) sao cho \(AB = 3AN,\;\,BC = 3MN.\) Khi đó:
A. \(\widehat {AMN} = \widehat {ANM}.\)
B. \(\widehat {AMN} = \widehat C.\)
C. \(\widehat {AMN} = \widehat B.\)
D. \(\widehat {ANM} = \widehat C.\)
Quảng cáo
Trả lời:
Giải bởi Vietjack
Đáp án đúng là: B
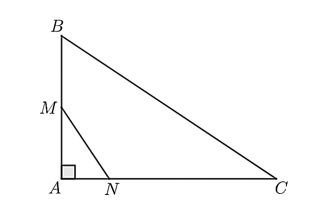
Vì \(\Delta ABC\) và \(\Delta ANM\) có: \(\frac{{AB}}{{AN}} = \frac{{BC}}{{NM}}\;\,\left( { = \frac{1}{3}} \right),\;\,\widehat {BAC} = \widehat {NAM} = 90^\circ \) nên
Do đó, \(\widehat {AMN} = \widehat C,\;\,\widehat {ANM} = \widehat B.\) Suy ra, chọn đáp án B.
Hot: 1000+ Đề thi cuối kì 1 file word cấu trúc mới 2025 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
Sách thầy cô Vietjack biên soạn:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Đáp án đúng là: C
\(\Delta ADC\) và \(\Delta AEB\) có: \(\widehat {DAC} = \widehat {EAB} = 90^\circ ,\;\,\frac{{AD}}{{AE}} = \frac{{AC}}{{AB}}\;\,\left( {{\rm{do}}\;\,\frac{2}{4} = \frac{1}{2}} \right)\) nên
Câu 2
A. \(20\;{\rm{m}}{\rm{.}}\)
B. \(25\;{\rm{m}}{\rm{.}}\)
C. \(30\;\,{\rm{m}}{\rm{.}}\)
D. \(16\;{\rm{m}}{\rm{.}}\)
Lời giải
Đáp án đúng là: C
\(\Delta ABC\) và \(\Delta AMN\) có: \(\widehat {MNA} = \widehat {ACB} = 90^\circ ,\;\,\widehat A\) chung. Do đó,
Suy ra \(\frac{{BC}}{{NM}} = \frac{{AC}}{{AN}} = \frac{{40}}{4} = 10.\) Do đó, \(BC = 10MN = 10 \cdot 3 = 30\;\,\left( {\rm{m}} \right).\)
Vậy chiều cao của ngọn tháp bằng \(30\;\,{\rm{m}}{\rm{.}}\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. Một góc nhọn của tam giác vuông này bằng một góc nhọn của tam giác vuông kia.
B. Hai cạnh góc vuông của tam giác này tỉ lệ với hai cạnh góc vuông của tam giác kia.
C. Cạnh góc vuông và cạnh huyền của tam giác vuông này tỉ lệ với cạnh góc vuông và cạnh huyền của tam giác vuông.
D. Cạnh huyền của tam giác này bằng cạnh huyền của tam giác kia.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. \(\widehat M = \frac{3}{4}\widehat B.\)
B. \(\widehat M = \frac{2}{3}\widehat B.\)
C. \(\widehat M = \widehat C.\)
D. \(\widehat M = \widehat B.\)
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo