Bạn Hà có 42 viên bi màu đỏ và 30 viên bi màu vàng. Hà có thể chia nhiều nhất vào bao nhiêu túi sao cho số bi đỏ và bi vàng được chia đều vào các túi? Khi đó, mỗi túi có bao nhiêu viên bi đỏ và vàng?
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 6 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Gọi \[x\] là số túi bi chia được nhiều nhất \((x \in \mathbb{N}*)\).
Vì số bi đỏ và vàng mỗi túi là đều nhau nên \(42\,\, \vdots \,\,x\) và \(30\,\, \vdots \,\,x\).
Do đó \[x\] là ƯC\[\left( {42,\,\,30} \right)\].
Mặt khác \[x\] lớn nhất (chia vào nhiều túi nhất) nên \[x\] là ƯCLN\[\left( {42,\,\,30} \right)\].
Ta có: \[42 = 2\,\,.\,\,3\,\,.\,\,7\,;{\rm{ }}30 = 2\,\,.\,\,3\,\,.\,\,5\].
ƯCLN\[\left( {42,\,\,30} \right) = 2\,\,.\,\,3 = 6\].
Do đó \[x = 6\]. Khi đó:
Số bi màu đỏ mỗi túi là: \[42:6 = 7\] (viên).
Số bi màu vàng mỗi túi là: \[30:6 = 5\] (viên).
Vậy Hà có thể chia nhiều nhất vào 6 túi. Khi đó, mỗi túi có 7 viên bi đỏ và 5 viên bi vàng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 2
Hình vuông \[ABCD\] có bốn cạnh bằng nhau: \[AB = BC = CD = AD\]
Hình vuông \[ABCD\] có bốn góc ở đỉnh \[A;\,\,B;\,\,C;\,\,D\] bằng nhau
Hình vuông \[ABCD\] có hai đường chéo bằng nhau: \[AC = BD\]
Hình vuông \[ABCD\] có hai cặp cạnh đối song song \[AB\] và \[BC\]; \[CD\] và \[AD\].
Lời giải
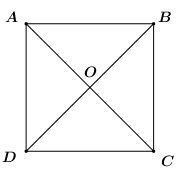
Đáp án đúng là: D
Khẳng định D sai vì \[AB\] và \[BC\]; \[CD\] và \[AD\] không phải các cạnh đối nên nó không song song.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
10 cm
12 cm
36 cm
24 cm.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
![Tìm x , biết: (a) [ 43 − ( 56 − x ) ] . 12 = 384 (ảnh 1)](https://video.vietjack.com/upload2/images/1762952025/image4.png)