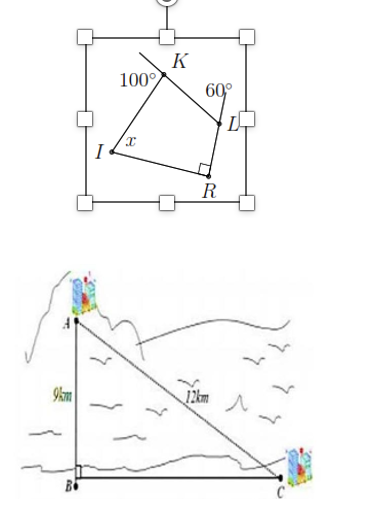
a) Tìm \(x\) trong hình vẽ bên.
b) Một công ty muốn làm một đường ống dẫn từ nhà máy \(C\) trên bờ biển đến một điểm \(B\) trên đất liền. Điểm \(A\) trên đảo cách điểm \(B\) là \(9\,\;{\rm{km}}.\) Giá để xây dựng đường ống từ nhà máy (điểm \(C)\) đến điểm \(B\) trên đất liền là \(5\,\,000\,\,{\rm{USD}}/{\rm{km}}.\) Khoảng cách từ \(A\) đến \(C\) là \(12\;\,{\rm{km}}{\rm{.}}\) Em hãy tính chi phí làm đường ống từ điểm \(C\) tới điểm \(B\) của công ty trên bằng tiền VNĐ (kết quả làm tròn đến hàng nghìn). Biết \(1\,\,{\rm{USD}} = 24\,\,300\) VNĐ tại thời điểm đó.
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 8 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Vì góc ngoài tại đỉnh \(K\) của tứ giác \(IKLR\) có số đo là \(100^\circ \) nên \(\widehat {IKL} = 180^\circ - 100^\circ = 80^\circ \).
Góc ngoài tại đỉnh \(L\) của tứ giác \(IKLR\) có số đo là \(60^\circ \) nên \(\widehat {KLR} = 180^\circ - 60^\circ = 120^\circ \).
Ta có tổng các góc trong tứ giác \(IKLR\) là \(360^\circ \) nên \(\widehat {IKL} + \widehat {KLR} + \widehat {R\,} + \widehat {I\,} = 360^\circ \)
Suy ra \(80^\circ + 120^\circ + 90^\circ + x = 360^\circ \)
Do đó \(x = 70^\circ \).
b) Áp dụng định lý Pythagore vào tam giác vuông \(ABC\) vuông tại \(B\) ta có:
\(A{C^2} = A{B^2} + B{C^2}\) suy ra \(B{C^2} = A{C^2} - A{B^2} = {12^2} - {9^2} = 144 - 81 = 63\)
Suy ra \(BC = \sqrt {63} \) (km).
Chi phí làm đường ống từ \(C\) tới điểm \(B\) của công ty trên bằng tiền VNĐ là:
\(\sqrt {63} \cdot 5\,\,000 \cdot 24\,\,300 \approx 964\,\,376\,\,352,9\) (VNĐ) \( \approx 964\,\,376\,\,000\) (VNĐ).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
\[P = \frac{1}{{x - 1}} + \frac{x}{{{x^2} + x + 1}} + \frac{{2x + 1}}{{1 - {x^3}}}\] với \(x \ne 1.\)
a) Với \(x \ne 1\) ta có:
\[P = \frac{1}{{x - 1}} + \frac{x}{{{x^2} + x + 1}} + \frac{{2x + 1}}{{1 - {x^3}}}\]
\[ = \frac{1}{{x - 1}} + \frac{x}{{{x^2} + x + 1}} - \frac{{2x + 1}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\]
\( = \frac{{{x^2} + x + 1 + x\left( {x - 1} \right) - 2x - 1}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)
\( = \frac{{{x^2} + x + 1 + {x^2} - x - 2x - 1}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)
\( = \frac{{2{x^2} - 2x}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}} = \frac{{2x\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {{x^2} + x + 1} \right)}}\)
\( = \frac{{2x}}{{{x^2} + x + 1}}\).
Vậy với \(x \ne 1\) thì \(P = \frac{{2x}}{{{x^2} + x + 1}}.\)
b) Với \(x = 2\) (thỏa mãn) thay vào biểu thức \(P\) ta được: \(P = \frac{{2 \cdot 2}}{{{2^2} + 2 + 1}} = \frac{4}{7}.\)
c) Với \(x > 0,x \ne 1\) ta có:
⦁ \(2x > 0;\)
⦁ \({x^2} + x + 1 = {x^2} + x + \frac{1}{4} + \frac{3}{4} = {\left( {x + \frac{1}{2}} \right)^2} + \frac{3}{4} > 0.\)
Do đó \(P = \frac{{2x}}{{{{\left( {x + \frac{1}{2}} \right)}^2} + \frac{3}{4}}} > 0\) với mọi \(x > 0,x \ne 1\).
Câu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đáp án đúng là: A
Ta có: \({\left( {x - 5} \right)^2} - {\left( {x + 5} \right)^2} = \left( {x - 5 + x + 5} \right)\left( {x - 5 - x - 5} \right) = 2x \cdot \left( { - 10} \right) = - 20x\).
Câu 3
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập