Cho \(A = 7 + {7^2} + {7^3} + ... + {7^{119}} + {7^{120}}\). Chứng minh rằng biểu thức \[A\] chia cho hết cho 57.

Gọi \[x\] (túi) là số túi bi chia được nhiều nhất \((x \in \mathbb{N}*)\).

Vì số bi đỏ và vàng mỗi túi là đều nhau nên \(42\,\, \vdots \,\,x\) và \(30\,\, \vdots \,\,x\).

Do đó \[x\] là ƯC\[\left( {42,\,\,30} \right)\].

Mặt khác \[x\] lớn nhất (chia vào nhiều túi nhất) nên \[x\] là ƯCLN\[\left( {42,\,\,30} \right)\].

Ta có: \[42 = 2\,\,.\,\,3\,\,.\,\,7\,;{\rm{ }}30 = 2\,\,.\,\,3\,\,.\,\,5\].

ƯCLN\[\left( {42,\,\,30} \right) = 2\,\,.\,\,3 = 6\].

Do đó \[x = 6\]. Khi đó:

Số bi màu đỏ mỗi túi là: \[42:6 = 7\] (viên).

Số bi màu vàng mỗi túi là: \[30:6 = 5\] (viên).

Vậy Hà có thể chia nhiều nhất vào 6 túi. Khi đó, mỗi túi có 7 viên bi đỏ và 5 viên bi vàng.

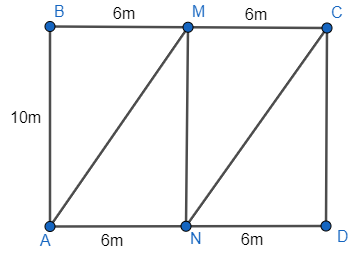
a) Dễ thấy trong hình bình hành \[AMCN\] chiều cao tương ứng của cạnh \[AN\] là \[MN\] và \[MN = AB = 10\] m.

Do đó diện tích hình bình hành \[AMCN\] là: \[6\,\,.{\rm{ }}10 = 60\] (m²)

Diện tích hình chữ nhật \[ABCD\] là: \[10\,\,.{\rm{ }}12 = 120\] (m²)

Phần diện tích còn lại trồng cỏ là: \[120 - 60 = 60\] (m²)

b) Số tiền công cần để chi trả trồng hoa là: 

\[50{\rm{ }}000\,\,.{\rm{ }}60 = 3{\rm{ }}000{\rm{ }}000\] (đồng)

Số tiền công cần để chi trả trồng cỏ là: 

\[40{\rm{ }}000\,\,.{\rm{ }}60 = 2{\rm{ }}400{\rm{ }}000\] (đồng)

Số tiền công cần để chi trả trồng hoa và cỏ là:

\[3{\rm{ }}000{\rm{ }}000 + 2{\rm{ }}400{\rm{ }}000 = 5{\rm{ }}400{\rm{ }}000\] (đồng).

Vậy số tiền công cần để chi trả trồng hoa và cỏ là \[5{\rm{ }}400{\rm{ }}000\] đồng.