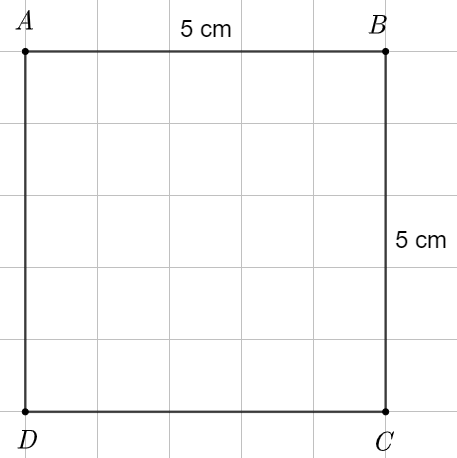
(a) Vẽ hình vuông \[MNPQ\] biết độ dài một cạnh bằng 5 cm.
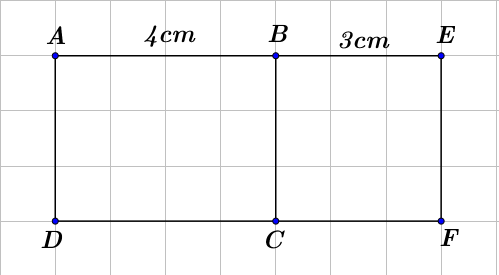
(b) Cho hình vẽ, biết \[ABCD\] là hình chữ nhật và \[BEFC\] là hình vuông. Biết \[AB\; = 4\] cm và \[BE = 3\] cm. Tính diện tích hình chữ nhật \[AEFD\].
Câu hỏi trong đề: Bộ 10 đề thi giữa kì 1 Toán 6 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Hình vuông \[MNPQ\] có độ dài một cạnh bằng 5 cm (như hình vẽ).
b)
Vì \[BEFC\] là hình vuông nên \(BE = EF = 3\) cm.
Diện tích hình chữ nhật \[ABCD\] là: \(4\,\,.\,\,3 = 12\) (cm2).
Diện tích hình vuông \[BEFC\] là: \({3^2} = 9\) (cm2).
Diện tích hình chữ nhật \[AEFD\] là: \(12 + 9 = 21\) (cm2).
Vậy diện tích hình chữ nhật \[AEFD\] bằng 21 cm2.
Hot: Giáo án năng lực số, PPT AI khởi động lớp 1-12 (Update 2026) (chỉ từ 150k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
Hai cạnh đối bằng nhau
Hai cạnh đối song song
Hai góc đối bằng nhau
Hai đường chéo bằng nhau.
Lời giải
Đáp án đúng là: D
Yếu tố không phải của hình bình hành là: Hai đường chéo bằng nhau.
Câu 2
\(AB,CD,AC\)
\(AD,FC,EB\)
\(AB,CD,EF\)
\(FE,ED,DC\).
Lời giải
Đáp án đúng là: B
Ba đường chéo chính của lục giác \(ABCDEF\) là \[AD,\,\,FC,\,\,\,EB\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
\(\mathbb{N} = \left\{ {1;\,\,2;\,\,3;\,\,4;\,\,...} \right\}\)
\[\mathbb{N} = \left\{ {0;\,\,1;\,\,2;\,\,3;\,\,4;\,...} \right\}\]
\(\mathbb{N} = \left\{ {0;\,\,1;\,\,2;\,\,3;\,\,4} \right\}\)
\(\mathbb{N} = \left\{ {1;\,\,2;\,\,3;\,\,4} \right\}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
\[\left( {a + b + c} \right)\,\, \vdots \,\,3\]
\[\left( {a + b + c} \right)\,\, \vdots \,\,6\]
\[\left( {a + b + c} \right)\,\, \vdots \,\,9\]
\[\left( {a + b + c} \right)\,\, \vdots \,\,27\].
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập