Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\frac{1}{4}x + \frac{1}{4}\;\;\;\;\;\;\;\;{\rm{khi}}\;\;x \le 2\\\frac{{\sqrt {3x - 2} - 2}}{{x - 2}}\;\;{\rm{khi}}\;\;x > 2\end{array} \right.\).
\(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \frac{1}{2}\).
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \frac{1}{4}\).
Hàm số \(f\left( x \right)\) liên tục tại \(x = 2\).
\(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \frac{3}{4}\).
Câu hỏi trong đề: Đề kiểm tra Toán 11 Chân trời sáng tạo Chương 3 có đáp án !!
Quảng cáo
Trả lời:
a) \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{\sqrt {3x - 2} - 2}}{{x - 2}} = \mathop {\lim }\limits_{x \to {2^ + }} \frac{{3\left( {x - 2} \right)}}{{\left( {x - 2} \right)\left( {\sqrt {3x - 2} + 2} \right)}}\)\( = \mathop {\lim }\limits_{x \to {2^ + }} \frac{3}{{\sqrt {3x - 2} + 2}} = \frac{3}{4}\).
b) \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \left( {\frac{1}{4}x + \frac{1}{4}} \right)\)\( = \frac{1}{4}\).
c) \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{1}{4}x + \frac{1}{4}} \right) = \frac{3}{4}\).
Có \(f\left( 2 \right) = \frac{3}{4}\).
Vì \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = f\left( 2 \right)\). Do đó hàm số liên tục tại \(x = 2\).
d) \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {\frac{1}{4}x + \frac{1}{4}} \right) = \frac{3}{4}\)
Đáp án: a) Sai; b) Đúng; c) Đúng; d) Đúng.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
- Sách - Sổ tay kiến thức trọng tâm Vật lí 11 VietJack - Sách 2025 theo chương trình mới cho 2k8 ( 45.000₫ )
- Trọng tâm Hóa học 11 dùng cho cả 3 bộ sách Kết nối, Cánh diều, Chân trời sáng tạo VietJack - Sách 2025 ( 58.000₫ )
- Sách lớp 11 - Trọng tâm Toán, Lý, Hóa, Sử, Địa lớp 11 3 bộ sách KNTT, CTST, CD VietJack ( 52.000₫ )
- Sách lớp 10 - Combo Trọng tâm Toán, Văn, Anh và Lí, Hóa, Sinh cho cả 3 bộ KNTT, CD, CTST VietJack ( 75.000₫ )
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
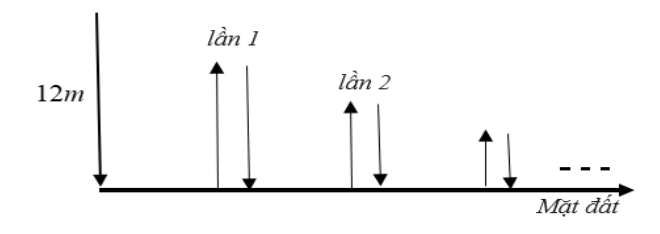
Ta coi độ cao nảy lên lần thứ nhất là \({u_1} \Rightarrow {u_1} = 12 \cdot \frac{2}{3} = 8\).
Khi đó \({u_2} = \frac{2}{3}{u_1};{u_3} = \frac{2}{3}{u_2};....\)
Đây là cấp số nhân lùi vô hạn với \({u_1} = 8;q = \frac{2}{3}\).
Khi đó tổng quãng đường quả bóng di chuyển là
\(S = 12 + 2{u_1} + 2{u_2} + ... + 2{u_n} + ...\)\( = 12 + 2\left( {{u_1} + {u_2} + ... + {u_n} + ...} \right) = 12 + 2 \cdot \frac{{{u_1}}}{{1 - q}}\)\( = 12 + 2 \cdot \frac{8}{{1 - \frac{2}{3}}} = 60\).
Trả lời: 60.
Câu 2
\(\mathbb{R}\).
\(\left( { - 3; + \infty } \right)\).
\(\left( { - \infty ;2} \right) \cup \left( {2; + \infty } \right)\).
\(\left( { - \infty ;3} \right)\).
Lời giải
Tập xác định của hàm số là \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
Do đó hàm số liên tục trên khoảng \(\left( { - \infty ;2} \right) \cup \left( {2; + \infty } \right)\). Chọn C.
Câu 3
\({x_0} = 4\).
\({x_0} = 0\).
\({x_0} = 2\).
\({x_0} = 3\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
\(f\left( 8 \right) = - \frac{1}{5}\).
\(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \frac{1}{3}\).
\(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = \frac{1}{6}\).
Biết \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = a,\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + x + 2} - x} \right) = b\). Khi đó \(3a + 4b = 2\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.