Trong các khẳng định sau, khẳng định nào là sai?
Trong các khẳng định sau, khẳng định nào là sai?
Câu hỏi trong đề: Bộ 10 đề thi Cuối kì 1 Toán 8 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Hướng dẫn giải:
Đáp án đúng là: D
Khẳng định sai là: Trong hình chữ nhật có hai cạnh kề bằng nhau.
Chẳng hạn: Tứ giác có 3 góc vuông và hai cạnh kề không bằng nhau thì hình đó cũng là hình chữ nhật.

Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Hướng dẫn giải
Ta có: \(M = 2{x^2} + 4{y^2} + 6x - 4y + 2024\)
\( = \left( {{x^2} + 4x + 4} \right) + \left( {{x^2} + 4{y^2} + 1 + 2x - 4xy - 4y} \right) + 2019\)
\( = \left( {{x^2} + 4x + {2^2}} \right) + \left[ {{x^2} + {{\left( {2y} \right)}^2} + {1^2} + 2x - 2.x.2y - 2.2y} \right] + 2019\)
\( = {\left( {x + 2} \right)^2} + {\left( {x - 2y + 1} \right)^2} + 2019\).
Với mọi \(x,\,\,y \in \mathbb{R}\), ta có: \({\left( {x + 2} \right)^2} \ge 0;\) \({\left( {x - 2y + 1} \right)^2} \ge 0\).
Do đó \(M = {\left( {x + 2} \right)^2} + {\left( {x - 2y + 1} \right)^2} + 2019 \ge 2019\).
Dấu xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}{\left( {x + 2} \right)^2} = 0\\{\left( {x - 2y + 1} \right)^2} = 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}x + 2 = 0\\x - 2y + 1 = 0\end{array} \right.\) nên \(\left\{ \begin{array}{l}x = - 2\\y = \frac{{ - 1}}{2}\end{array} \right.\).
Vậy giá trị nhỏ nhất của biểu thức \(M\) là 2019 khi \(x = - 2\) và \(y = \frac{{ - 1}}{2}.\)
Lời giải
Hướng dẫn giải
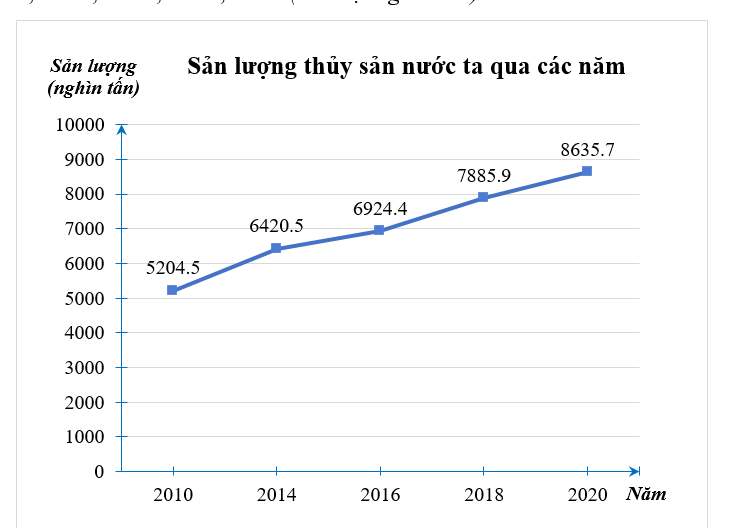
a) Ta có bảng thống kê sản lượng thủy sản nước ta qua các năm 2010; 2014; 2016; 2018; 2020 như sau:
|
Năm |
2010 |
2014 |
2016 |
2018 |
2020 |
|
Sản lượng (nghìn tấn) |
\[5\,\,204,5\] |
\[6\,\,420,5\] |
\[6\,\,924,4\] |
\[7\,\,885,9\] |
\[8\,\,635,7\] |
b) Dựa vào thống kê, ta có:
- Năm 2020 sản lượng thủy sản nước ta cao nhất (\[8\,\,635,7\] nghìn tấn).
- Năm 2010 sản lượng thủy sản nước ta thấp nhất (\[5\,\,204,5\] nghìn tấn).
Câu 3
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.