PHẦN II. TỰ LUẬN (7,0 điểm)

 (1,0 điểm) Cho đa thức \(A = 3{x^2}y - 2x{y^2} - 4xy + 1.\)

a) Tìm đa thức \(B\) sao cho \(B - A = - 2{x^3}y + 7{x^2}y + 3xy.\)

b) Tìm đa thức \(M\) sao cho \(A + M = 3{x^2}{y^2} - 5{x^2}y + 8xy\).

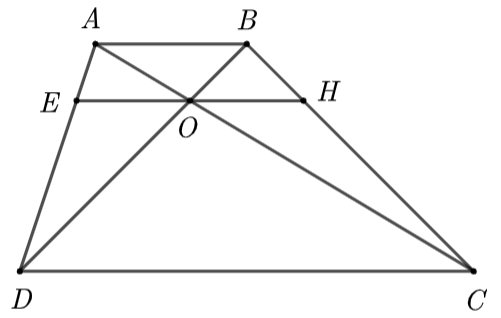
Ta có \(EH\,{\rm{//}}\,AB\) mà \(AB\,{\rm{//}}\,CD\) nên \(EH\,{\rm{//}}\,CD.\)

• Xét \(\Delta ACD\) có \[OE{\rm{ // }}CD\] \[\left( {O\;\, \in EH,{\rm{ }}EH{\rm{// }}CD} \right)\], áp dụng hệ quả của định lí Thalès, ta có: $\frac{AO}{AC}=\frac{OE}{DC}\left(1\right)$

• Xét \(\Delta BCD\) có \[OH{\rm{ // }}CD\] \[\left( {O\,\; \in EH,{\rm{ }}EH{\rm{// }}CD} \right)\], áp dụng hệ quả của định lí Thalès, ta có: $\frac{OH}{DC}=\frac{HB}{BC}\left(2\right)$

• Xét \(\Delta ABC\) có \[OH{\rm{ // }}AB\] \[\left( {O\,\; \in EH,{\rm{ }}EH{\rm{// }}AB} \right)\], áp dụng định lí Thalès, ta có: $\frac{AO}{AC}=\frac{HB}{BC}\left(3\right)$

Từ (1), (2) và (3) suy ra \[\frac{{OH}}{{DC}} = \frac{{OE}}{{DC}}\] .

Do đó \[OE = OH\] (đpcm).

Hướng dẫn giải

Ta có \(A = x\left( {x - 7} \right)\left( {x - 3} \right)\left( {x - 4} \right) = \left( {{x^2} - 7x} \right)\left( {{x^2} - 7x + 12} \right)\).     

Đặt \(t = {x^2} - 7x + 6\), khi đó:

\(A = \left( {t - 6} \right)\left( {t + 6} \right) = {t^2} - 36 \ge - 36\).

Dấu  khi \({t^2} = 0\) hay \({x^2} - 7x + 6 = 0\)

\[\left( {{x^2} - x} \right) - \left( {6x - 6} \right) = 0\]

\[x\left( {x - 1} \right) - 6\left( {x - 1} \right) = 0\]

\[\left( {x - 1} \right)\left( {x - 6} \right) = 0\]

Suy ra \(x = 1\) hoặc \(x = 6\).

Vậy giá trị nhỏ nhất của biểu thức \[A\] bằng \( - 36\) khi \(x = 1\) hoặc \(x = 6\).