(1,5 điểm) Biểu đồ cột biểu diễn sản lượng khoai lang ở Phú Thọ qua các năm 2015; 2018; 2019; 2020 (đơn vị: nghìn tấn):
a) Biểu đồ trên là biểu đồ gì? Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập trực tiếp hay gián tiếp?
b) Năm 2019 sản lượng khoai lang ở Phú Thọ tăng hay giảm bao nhiêu phần trăm so với năm 2015 (làm tròn kết quả đến hàng phần mười)? Em có nhận xét gì về sản lượng khoai lang ở Phú Thọ qua các năm 2015; 2018; 2019; 2020.
c) Một bài báo đã nêu nhận định sau: “Năm 2020 sản lượng khoai lang ở Phú Thọ là ít nhất, năm 2020 sản lượng khoai lang ở Phú Thọ giảm \[19,2\% \] so với năm 2018”. Theo em, nhận định của bài báo đó có chính xác không?
(1,5 điểm) Biểu đồ cột biểu diễn sản lượng khoai lang ở Phú Thọ qua các năm 2015; 2018; 2019; 2020 (đơn vị: nghìn tấn):
a) Biểu đồ trên là biểu đồ gì? Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập trực tiếp hay gián tiếp?
b) Năm 2019 sản lượng khoai lang ở Phú Thọ tăng hay giảm bao nhiêu phần trăm so với năm 2015 (làm tròn kết quả đến hàng phần mười)? Em có nhận xét gì về sản lượng khoai lang ở Phú Thọ qua các năm 2015; 2018; 2019; 2020.
c) Một bài báo đã nêu nhận định sau: “Năm 2020 sản lượng khoai lang ở Phú Thọ là ít nhất, năm 2020 sản lượng khoai lang ở Phú Thọ giảm \[19,2\% \] so với năm 2018”. Theo em, nhận định của bài báo đó có chính xác không?
Câu hỏi trong đề: Bộ 10 đề thi Cuối kì 1 Toán 8 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải
a) Biểu đồ đã cho là biểu đồ cột.
Để thu được dữ liệu được biểu diễn ở biểu đồ trên, ta sử dụng phương pháp thu thập gián tiếp bằng cách truy cập website của Niên giám thống kê 2021.
b) Ta thấy sản lượng khoai lang Phú Thọ năm 2019 nhỏ hơn sản lượng khoai lang Phú Thọ năm 2015 (vì \(10,2 < 14,5\)).
Do đó, sản lượng khoai lang Phú Thọ năm 2019 giảm so với năm 2015.
Tỉ số phần trăm sản lượng khoai lang ở Phú Thọ trong năm 2019 so với năm 2015 là: \(\frac{{10,2}}{{14,5}} \cdot 100\% \approx 70,3\% \).
Vậy năm 2019 sản lượng khoai lang ở Phú Thọ tăng khoảng \(100\% - 70,3\% = 29,7\% \) so với năm 2015.
c) Năm 2020 sản lượng khoai lang ở Phú Thọ là 8,4 nghìn tấn ít nhất so với các năm còn lại.
Tỉ số phần trăm sản lượng khoai lang ở Phú Thọ năm 2020 so với năm 2018 là:
\(\frac{{8,4}}{{10,4}} = 80,8\% \).
Năm 2020 sản lượng khoai lang ở Phú Thọ giảm \[19,2\% \] so với năm 2018.
Theo em nhận định của bài báo đó chính xác.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải:
1. Xét \(\Delta ABC\) vuông tại \[A\], theo định lý Pythagore, ta có:
\(A{B^2} + A{C^2} = B{C^2}\)
Suy ra \[A{C^2} = B{C^2} - A{B^{2\;}} = {100^2} - {60^2} = 6400\].
Khi đó \[AC = \sqrt {6\,400} = 80\,\,{\rm{(cm)}}\]
Vì \[80\,\,{\rm{cm}} < 85\,\,{\rm{cm}}\] nên nhà bạn Nam đã thực hiện đúng quy định của khu phố.
2.
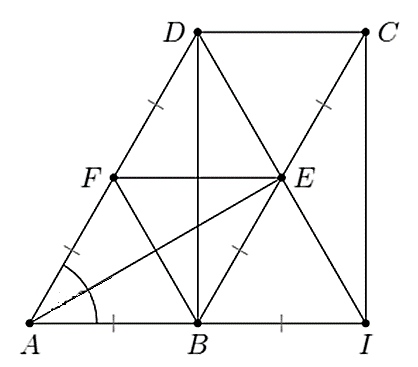
a) Do \(E\) là trung điểm của \(BC\) nên \(BE = \frac{1}{2}BC\) hay \(BC = 2BE.\)
Vì \(BC = 2AB\) và \(BC = 2BE\) nên \(AB = BE\).
Theo đề bài, tứ giác \(ABCD\) là hình bình hành nên \(AD = BC,\,\,AD\,{\rm{//}}\,BC\).
Vì \(AD = BC\); \(BE = \frac{1}{2}BC;\,AF = \frac{1}{2}AD\) (do \(F\) là trung điểm của \(AD)\) nên \(BE = AF\).
Tứ giác \(ABEF\) có \(BE = AF\) (cmt) và \(BE\,{\rm{//}}\,AF\) (vì \(AD\,{\rm{//}}\,BC\)).
Suy ra, tứ giác \(ABEF\) là hình bình hành.
Hình bình hành \(ABEF\) có \(AB = BE\) nên \(ABEF\) là hình thoi.
b) Vì tứ giác \(ABCD\) là hình bình hành nên \(AB = CD,\,\,AB\,{\rm{//}}\,CD\).
Vì \(AB = CD\); \(AB = BI\) (do \(B\) là trung điểm của \(AI)\) nên \(BI = CD\).
Tứ giác \(BICD\) có \(BI\,{\rm{//}}\,CD\) (vì \(AB\,{\rm{//}}\,CD\)) và \(BI = CD\) nên tứ giác \(BICD\) là hình bình hành.
Ta thấy \(BD\) vừa là đường trung tuyến vừa là đường phân giác của tam giác \(ADI\) nên tam giác \(ADI\) cân tại \(D\).
Tam giác \(ADI\) cân tại \(D\) có \(\widehat {DAI} = 60^\circ \) nên tam giác \(ADI\) là tam giác đều.
Suy ra \(BD\) cũng là đường cao của tam giác \(ADI\) nên \(BD \bot BI\) hay \(\widehat {DBI} = 90^\circ .\)
Hình bình hành \(BICD\) có \(\widehat {DBI} = 90^\circ \) nên tứ giác \(BICD\) là hình chữ nhật.
Khi đó, \(E\) là trung điểm của \(DI\).
Ta có tam giác \(ADI\) là tam giác đều có \(AE\) là đường trung tuyến nên đồng thời là đường cao.
Do đó, \(AE \bot DI\) hay \(\widehat {AED} = 90^\circ \).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
|
a) \({x^3}y + 2{x^2}y + xy\) \( = xy \cdot \left( {{x^2} + 2x + 1} \right)\) \( = xy \cdot {\left( {x + 1} \right)^2}.\) |
b) \({x^2} - 9 - 4xy + 4{y^2}\) \( = \left( {{x^2} - 4xy + 4{y^2}} \right) - 9\) \( = {\left( {x - 2y} \right)^2} - {3^2}\) \( = \left( {x - 2y - 3} \right)\left( {x - 2y + 3} \right).\) |
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập