Tứ giác \(ABCD\) là hình bình hành nếu thỏa mãn điều kiện nào dưới đây?
Tứ giác \(ABCD\) là hình bình hành nếu thỏa mãn điều kiện nào dưới đây?
Câu hỏi trong đề: Bộ 10 đề thi Cuối kì 1 Toán 8 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: D
• Tứ giác \(ABCD\) là hình bình hành nếu thỏa mãn điều kiện \[\widehat A = \widehat C;\,\,\widehat B = \widehat D\] (các góc đối bằng nhau).
• Tứ giác \(ABCD\) có một cặp cạnh đối bằng nhau \[\left( {AB = CD} \right)\] hoặc một cặp góc đối bằng nhau \[\left( {\widehat A = \widehat C} \right)\] thì chưa đủ điều kiện để kết luận hình bình hành.
• Tứ giác \(ABCD\) có một cặp cạnh đối song song \[\left( {AB\,{\rm{//}}\,CD} \right)\] thì chưa đủ để kết luận hình bình hành và hai đường chéo của hình bình hành có thể không bằng nhau.
Vậy ta chọn phương án D.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
Theo đề bài: \({x^2} + \frac{8}{{{x^2}}} + \frac{{{y^2}}}{8} = 8\) suy ra \(2{x^2} + \frac{{16}}{{{x^2}}} + \frac{{{y^2}}}{4} = 16\)
Ta có: \[2{x^2} + \frac{{16}}{{{x^2}}} + \frac{{{y^2}}}{4} = \left( {{x^2} + \frac{{16}}{{{x^2}}} - 8} \right) + \left( {{x^2} + \frac{{{y^2}}}{4} - xy} \right) + xy + 8\]
\[ = {\left( {x - \frac{4}{x}} \right)^2} + {\left( {x - \frac{y}{2}} \right)^2} + xy + 8\].
Vì \[{\left( {x - \frac{4}{x}} \right)^2} \ge 0\,;\,\,{\left( {x - \frac{y}{2}} \right)^2} \ge 0\] nên \[xy + 8 \le 16\] hay \[xy \le 8\].
Suy ra \(A = xy + 2023 \le 8 + 2023 = 2031\).
Dấu xảy ra khi và chỉ khi \(\left\{ \begin{array}{l}{\left( {x - \frac{4}{x}} \right)^2} = 0\\{\left( {x - \frac{y}{2}} \right)^2} = 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}x - \frac{4}{x} = 0\\x - \frac{y}{2} = 0\end{array} \right.\) nên \(\left\{ \begin{array}{l}{x^2} = 4\\y = 2x\end{array} \right.\).
Khi đó, \(x = 2\,;\,\,y = 4\) hoặc \(x = - 2\,;\,\,y = - \,4\).
Vậy giá trị lớn nhất của biểu thức \(A\) là 2031 khi \(x = 2\,;\,\,y = 4\) hoặc \(x = - 2\,;\,\,y = - \,4\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Hướng dẫn giải
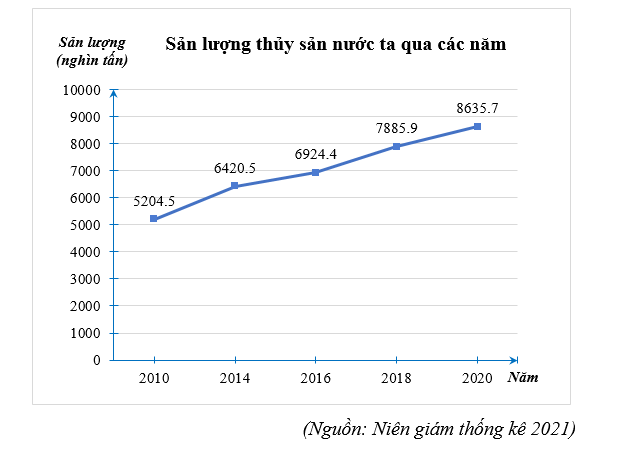
a) Ta có bảng thống kê sản lượng thủy sản nước ta qua các năm 2010; 2014; 2016; 2018; 2020 như sau:
|
Năm |
2010 |
2014 |
2016 |
2018 |
2020 |
|
Sản lượng (nghìn tấn) |
\[5\,\,204,5\] |
\[6\,\,420,5\] |
\[6\,\,924,4\] |
\[7\,\,885,9\] |
\[8\,\,635,7\] |
b) Dựa vào thống kê, ta có:
- Năm 2020 sản lượng thủy sản nước ta cao nhất (\[8\,\,635,7\] nghìn tấn).
- Năm 2010 sản lượng thủy sản nước ta thấp nhất (\[5\,\,204,5\] nghìn tấn).
c) Năm 2020 sản lượng thủy sản nước ta nhiều hơn năm 2014 là:
\(8\,\,635,7 - 6\,\,420,5 = 2\,\,215,2\) (nghìn tấn)
Năm 2020 sản lượng thủy sản nước ta gấp số lần so với năm 2014 là:
\(8\,\,635,7:6\,\,420,5 = 1,3\) (lần)
Vậy nhận định của bài báo đó là chính xác.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập