Tìm số nguyên \(n\) biết \(\left( {{n^2} + 2n - 3} \right) \vdots \left( {n + 1} \right)\).
Tìm số nguyên \(n\) biết \(\left( {{n^2} + 2n - 3} \right) \vdots \left( {n + 1} \right)\).
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 6 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
Ta có: \(\left( {{n^2} + 2n - 3} \right) \vdots \left( {n + 1} \right)\)
\(\left( {{n^2} + n + n + 1 - 4} \right) \vdots \left( {n + 1} \right)\)
\(\left[ {n\left( {n + 1} \right) + \left( {n + 1} \right) - 4} \right] \vdots \left( {n + 1} \right)\) \(\left( * \right)\)
Với mọi số nguyên \(n\) ta có: \(\left( {n + 1} \right) \vdots \left( {n + 1} \right)\)
Nên \(\left[ {n\left( {n + 1} \right) + \left( {n + 1} \right)} \right] \vdots \left( {n + 1} \right)\)
Do đó để \(\left( * \right)\) xảy ra thì \(4 \vdots \left( {n + 1} \right)\)
Khi đó \(n + 1\) là ước nguyên của 4.
Mà Ư\[\left( 4 \right) = \left\{ {1; - 1;2; - 2;4; - 4} \right\}\]
Ta có bảng sau:
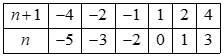
Đối chiếu điều kiện \(n\) là số nguyên, các giá trị ở trên đều thỏa mãn.
Vậy \(n \in \left\{ { - 5; - 3; - 2;0;1;3} \right\}\).
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi số học sinh của trường THCS đó là \(a\) (học sinh) \(\left( {a \in \mathbb{N},100 \le a < 250} \right)\).
Do khi xếp hàng 10 em thì thừa 8 em nên \(a\) chia 10 dư 8, hay \(\left( {a + 2} \right) \vdots 10\).
Khi xếp hàng 12 em thì thừa 10 em nên \(a\) chia 12 dư 10, hay \(\left( {a + 2} \right) \vdots 12\).
Khi xếp hàng 15 em thì thừa 13 em nên \(a\) chia 15 dư 13, hay \(\left( {a + 2} \right) \vdots 15\).
Từ đó suy ra \(a + 2 \in BC\left( {10,12,15} \right)\).
Ta có: \(10 = 2.5\); \(12 = {2^2}.3\); \(15 = 3.5\).
Do đó \(BCNN\left( {10,12,15} \right) = {2^2}.3.5 = 60\).
Khi đó \[a + 2 \in BC\left( {10,12,15} \right) = B\left( {60} \right) = \left\{ {0;60;120;180;240;300;360;...} \right\}\].
Mà \(100 \le a < 250\) nên \(102 \le a + 2 \le 252\), suy ra \(a + 2 \in \left\{ {120;180;240} \right\}\)
Do đó \(a \in \left\{ {118;178;238} \right\}\)
Mặt khác khi số học sinh của trường xếp hàng 17 thì vừa đủ nên \(a \vdots 17\)
Xét 3 trường hợp ở trên ta có \(a = 238\) thỏa mãn.
Vậy trường THCS đó có 238 học sinhCâu 2
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập