(1,0 điểm) Tìm \(x\), biết:

a) \(\frac{8}{5} - \frac{3}{5}:x = 0,4\);         

b) \(\frac{{\left| {2x - 1} \right|}}{5} = \frac{1}{4}\).

Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\frac{{a + b - c}}{c} = \frac{{b + c - a}}{a} = \frac{{c + a - b}}{b} = \frac{{a + b - c + b + c - a + c + a - b}}{{c + a + b}} = \frac{{a + b + c}}{{a + b + c}} = 1\)

Vì \(\frac{{a + b - c}}{c} = 1\) nên \(a + b - c = c\), suy ra \(a + b = 2c\).

Vì \(\frac{{b + c - a}}{a} = 1\) nên \(b + c - a = a\), suy ra \(b + c = 2a\).

Vì \(\frac{{c + a - b}}{b} = 1\) nên \(c + a - b = b\), suy ra \(c + a = 2b\).

Thay vào biểu thức \(P\) ta có:

\(P = \left( {1 + \frac{b}{a}} \right)\left( {1 + \frac{a}{c}} \right)\left( {1 + \frac{c}{b}} \right) = \frac{{a + b}}{a}.\frac{{c + a}}{c}.\frac{{b + c}}{b} = \frac{{2c}}{a}.\frac{{2b}}{c}.\frac{{2a}}{b} = \frac{{8abc}}{{abc}} = 8\)

Vậy \(P = 8\).

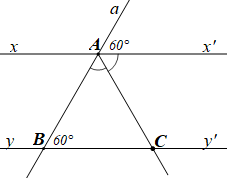
a) Học sinh vẽ lại hình theo đúng số đo các góc.

b) Ta có \[\widehat {aAx'} = \widehat {ABC}\] (cùng bằng \[60^\circ \])

Mà hai góc này ở vị trí đồng vị nên \(xx'\,{\rm{//}}\,yy'\).

c) Ta có \[\widehat {aAx'} + \widehat {BAx'} = 180^\circ \] (hai góc kề bù)

               \[\widehat {BAx'} = 180^\circ - \widehat {aAx'} = 180^\circ - 60^\circ = 120^\circ \]

Tia \(AC\) là tia phân giác của \(\widehat {BAx'}\) nên \(\widehat {BAC} = \widehat {CAx'} = \frac{1}{2}\widehat {BAx'} = 60^\circ \).

Do \(xx'\,{\rm{//}}\,yy'\) (chứng minh câu b) nên \(\widehat {ACB} = \widehat {CAx'} = 60^\circ \) (hai góc so le trong).