Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 6 Kết nối tri thức có đáp án !!
Quảng cáo
Trả lời:
Từ \(6{x^2} + 5{y^2} = 54\), suy ra \(6{x^2} \le 54\) (do \(5{y^2} \ge 0,\) với mọi \(y \in \mathbb{Z}\))
Suy ra \(0 \le {x^2} \le 9\), mà \(x \in \mathbb{Z}\) nên \({x^2} \in \mathbb{Z}\), do đó \({x^2} \in \left\{ {0;1;4;9} \right\}\)
Mặt khác, \({x^2} + 1 = 55 - 5{x^2} - 5{y^2}\), hiệu này chia hết cho 5
Do đó \(\left( {{x^2} + 1} \right) \vdots 5\), suy ra \({x^2} = 4\) hoặc \({x^2} = 9\)
Với \({x^2} = 4\), ta có \({y^2} = 6\) (loại, vì không thỏa mãn \(y \in \mathbb{Z}\))
Với \({x^2} = 9\), ta có: \({y^2} = 0\) suy ra \(y = 0\)
Khi đó \({x^2} = 9\) suy ra \(x = 3\) hoặc \(x = - 3\).
Vậy \(\left( {x;y} \right) \in \left\{ {\left( {3;0} \right);\left( { - 3;0} \right)} \right\}\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1
A. \(\left\{ {3;5;7;11;29} \right\}\);
B. \(\left\{ {0;3;5;7;13} \right\}\);
Lời giải
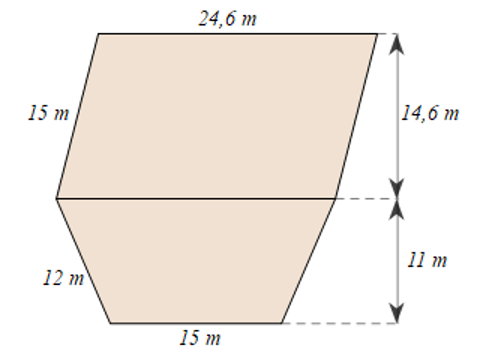
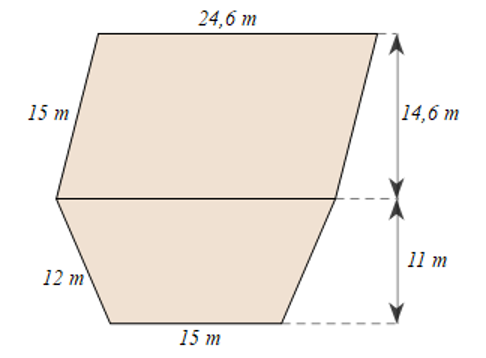
a) Diện tích phần ruộng hình bình hành là:
\(14,6.24,6 = 359,16\left( {{m^2}} \right)\)
Diện tích phần ruộng hình thang cân là:
\(\frac{{\left( {24,6 + 15} \right).11}}{2} = 217,8\left( {{m^2}} \right)\)
Diện tích thửa ruộng là:
\(359,16 + 217,8 = 576,96\left( {{m^2}} \right)\).
b) Mỗi vụ bác Lan thu hoạch được số kilôgam thóc là:
\(576,96.0,7 = 403,872\left( {kg} \right)\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. các số nguyên âm và các số nguyên dương;
B. số 0 và số nguyên âm;
C. số 0 và số nguyên dương;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Khối 6 của một trường THCS có 60 học sinh nam và 48 học sinh nữ. Các thầy, cô muốn chia học sinh khối 6 thành các nhóm để lao động trồng cây nhân dịp Tết Nguyên đán sao cho học sinh nam trong mỗi nhóm bằng nhau và số học sinh nữ trong mỗi nhóm cũng bằng nhau. Hỏi phải chia thành bao nhiêu nhóm để số học sinh trong mỗi nhóm là ít nhất? Khi đó mỗi nhóm có bao nhiêu học sinh nam và bao nhiêu học sinh nữ?
Khối 6 của một trường THCS có 60 học sinh nam và 48 học sinh nữ. Các thầy, cô muốn chia học sinh khối 6 thành các nhóm để lao động trồng cây nhân dịp Tết Nguyên đán sao cho học sinh nam trong mỗi nhóm bằng nhau và số học sinh nữ trong mỗi nhóm cũng bằng nhau. Hỏi phải chia thành bao nhiêu nhóm để số học sinh trong mỗi nhóm là ít nhất? Khi đó mỗi nhóm có bao nhiêu học sinh nam và bao nhiêu học sinh nữ?
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.