(1,5 điểm) Cho 3 đường thẳng \(a,\,b,\,c\) (như hình vẽ) biết \(a \bot c,\,b \bot c\).
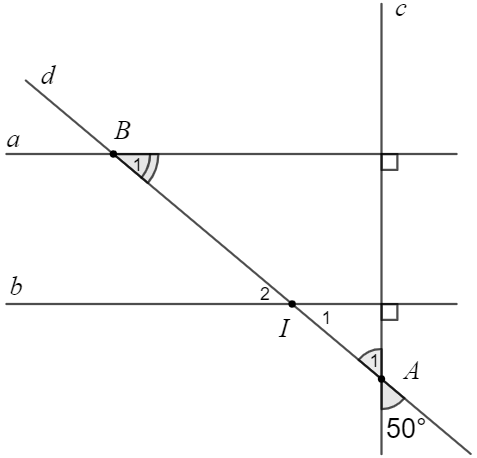
a) (0,5 điểm) Chứng minh \(a\,{\rm{//}}\,b\).
b) (1 điểm) Kẻ đường thẳng \(d\) tạo với đường thẳng \(c\) một góc \(50^\circ \) và cắt \(c\) tại điểm \(A\). \(d\) cắt \(a\) và \(b\) lần lượt tại \(B\) và \(I\). Tính \(\widehat {{B_1}}\).
(1,5 điểm) Cho 3 đường thẳng \(a,\,b,\,c\) (như hình vẽ) biết \(a \bot c,\,b \bot c\).
a) (0,5 điểm) Chứng minh \(a\,{\rm{//}}\,b\).
b) (1 điểm) Kẻ đường thẳng \(d\) tạo với đường thẳng \(c\) một góc \(50^\circ \) và cắt \(c\) tại điểm \(A\). \(d\) cắt \(a\) và \(b\) lần lượt tại \(B\) và \(I\). Tính \(\widehat {{B_1}}\).
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 7 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Vì hai đường thẳng phân biệt \(a\) và \(b\) cùng vuông góc với đường thẳng c nên suy ra \(a\) và \(b\) là hai đường thẳng song song.
Vậy \(a\,{\rm{//}}\,b\) (đpcm).
b) Đường thẳng \(d\) tạo với đường thẳng \(c\) một góc \(50^\circ \) và cắt \(c\) tại điểm \(A\) nên \(\widehat {{A_1}} = 50^\circ \).
\(\widehat {{I_1}}\) và \(\widehat {{A_1}}\) là hai góc phụ nhau nên \(\widehat {{I_1}} = 90^\circ - \widehat {{A_1}} = 90^\circ - 50^\circ = 40^\circ \).
Ta có \(a\,{\rm{//}}\,b\) nên suy ra \(\widehat {{I_1}} = \widehat {{B_1}} = 40^\circ \) (hai góc đồng vị).
Vậy \(\widehat {{B_1}} = 40^\circ \).
Hot: 1000+ Đề thi cuối kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Bể khi được bơm đầy nước có thể chứa được lượng nước là:
\({V_1} = 1,8\,\,.\,\,1,2\,\,.\,\,2 = 4,32\) (m3).
Sau khi dùng trong một ngày, lượng nước còn lại trong bể là:
\({V_2} = 1,8\,\,.\,\,1,2\,\,.\,\,1,3 = 2,808\) (m3).
Lượng nước đã dùng trong một ngày là:
\({V_1} - {V_2} = 4,32 - 2,808 = 1,512\) (m3).
Đổi: \(1,512\) m3 \( = 1\;512\) lít.
Vậy trong một ngày, thể tích nước đã dùng là 1 512 lít.
Câu 2
Lời giải
Đáp án đúng là: B
Căn bậc hai số học của \(196\) là \(\sqrt {196} = \sqrt {{{14}^2}} = 14\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 7
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Nhắn tin Zalo
Hỏi bài tập