Biểu đồ sau cho biết số cây trồng được của các lớp 6 trong một trường THCS nhân dịp lễ trông cây xanh:
\(6A\)
\(6B\)
\(6C\)
\(6D\)
: 10 cây
a) Lập bảng thống kê số cây xanh trồng được của mỗi lớp theo mẫu sau:
Lớp
\(6A\)
\(6B\)
\(6C\)
\(6D\)
Số cây xanh
b) Cả bốn lớp trồng được bao nhiêu cây? Chênh lệch số cây trồng được giữa lớp trồng được nhiều nhất và ít nhất là bao nhiêu?
Biểu đồ sau cho biết số cây trồng được của các lớp 6 trong một trường THCS nhân dịp lễ trông cây xanh:
|
\(6A\) |
|
|
\(6B\) |
|
|
\(6C\) |
|
|
\(6D\) |
|
|
|
|
a) Lập bảng thống kê số cây xanh trồng được của mỗi lớp theo mẫu sau:
|
Lớp |
\(6A\) |
\(6B\) |
\(6C\) |
\(6D\) |
|
Số cây xanh |
|
|
|
|
b) Cả bốn lớp trồng được bao nhiêu cây? Chênh lệch số cây trồng được giữa lớp trồng được nhiều nhất và ít nhất là bao nhiêu?
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 6 Chân trời sáng tạo có đáp án !!
Quảng cáo
Trả lời:
Giải bởi Vietjack
a) Số cây xanh lớp \(6A\) trồng được là: \(4.10 = 40\) (cây).
Số cây xanh lớp \(6B\) trồng được là: \(3.10 = 30\) (cây).
Số cây xanh lớp \(6C\) trồng được là: \(5.10 = 50\) (cây).
Số cây xanh lớp \(6D\) trồng được là: \(2.10 = 20\) (cây).
Ta lập được bảng thống kê số cây xanh trồng được của mỗi lớp như sau:
|
Lớp |
\(6A\) |
\(6B\) |
\(6C\) |
\(6D\) |
|
Số cây xanh |
40 |
30 |
50 |
20 |
b) Tổng số cây xanh trồng được của bốn lớp \(6A,6B,6C,6D\) là:
\(40 + 30 + 50 + 20 = 140\) (cây).
Lớp \(6C\) trồng được nhiều nhất, lớp \(6D\) trồng được ít nhất.
Lớp \(6C\) trồng được nhiều hơn lớp \(6D\) số cây là:
\(50 - 20 = 30\) (cây)
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Đang tải chế độ Học...
Hot: 1000+ đề thi giữa kì 1 lớp 1-12 đầy đủ các môn (Update 2026) (chỉ từ 60k). Tải ngay
Đăng ký VIP để học và luyện thi không giới hạn
Trọn bộ quyền lợi trên Vietjack, trong một tài khoản.
- Phòng luyện thi cấp tốc: ĐGNL - ĐGTD, Tốt nghiệp THPT, Ôn vào 10, Ôn vào 6, Ôn Giữa kì/Cuối kì
- Hơn 200K đề thi thử, đề minh hoạ, chính thức các năm
- Với 3tr+ câu hỏi theo các mức độ Nhận biết, Thông hiểu, Vận dụng
- Tải xuống đề thi [DOCX] với đầy đủ đáp án
- Xem hàng ngàn bài giảng đính kèm củng cố thêm kiến thức
- Bao gồm tất cả các bậc từ Tiểu học đến Đại học
- Chặn hiển thị quảng cáo tăng khả năng tập trung ôn luyện
- Đăng ký ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Gọi số người của đơn vị đó là \(a\) (người) \(\left( {a \in \mathbb{N},320 < a < 400} \right)\).
Vì khi xếp hàng 10; 12 hoặc 15 đều thừa ra 5 người nên \(a:10;\,\,a:12;\,\,a:15\) đều dư 5
Suy ra \(\left( {a - 5} \right) \vdots 10;\,\,\left( {a - 5} \right) \vdots 12;\,\,\left( {a - 5} \right) \vdots 15\)
Hay \(a - 5 \in BC\left( {10,12,15} \right)\)
Ta có: \(10 = 2.5;\) \(12 = {2^2}.3\); \(15 = 3.5\).
Do đó \(BCNN\left( {10,12,15} \right) = {2^2}.3.5 = 60\)
Suy ra \(a - 5 \in BC\left( {10,12,15} \right) = B\left( {60} \right) = \left\{ {0;60;120;180;240;300;360;420;...} \right\}\)
Khi đó \(a \in \left\{ {5;65;125;185;245;305;365;425;...} \right\}\)
Mà \(320 < a < 400\) nên \(a = 365\).
Vậy đơn vị bộ đội có 365 người.
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Với \(x,y\) là số nguyên, từ \(\left( {x + 5} \right)\left( {2y + 1} \right) = 4\), suy ra \(2y + 1\) là ước của 4.
Mà Ư\(\left( 4 \right) = \left\{ {1; - 1;2; - 2;4; - 4} \right\}\).
Do \(y\) là số nguyên nên \(2y + 1\) là số lẻ nên \(2y + 1\) chỉ là ước lẻ của 4.
Khi đó \(2y + 1 \in \left\{ {1; - 1} \right\}\).
Ta có bảng sau:
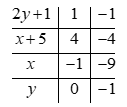
Vậy \[\left( {x;y} \right) \in \left\{ {\left( { - 1;0} \right);\left( { - 9; - 1} \right)} \right\}\].
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
A. Rắn, gà, chó, trâu, bò;
B. Chó, mèo, gà, vịt;
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Bạn Bình bị viễn thị \(1,25\) điốp;
B. Bạn Bình bị cận thị \(1,25\) điốp;
Đăng nhập để xem lời giải
Lưu tiến độ và luyện tập hiệu quả hơn. Hoàn toàn miễn phí!
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 250K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Đăng ký để học cùng Vietjack. Hoàn toàn miễn phí!
Bằng việc đăng ký, bạn đồng ý với Điều khoản sử dụng và Chính sách bảo mật của Vietjack.
Nhắn tin Zalo
Hỏi bài tập