Thực hiện phép tính (tính hợp lí nếu có thể):
a) \(160 - \left( {{{4.5}^2} - {{3.2}^3}} \right)\);
b) \(43 + \left( { - 100} \right) + \left( { - 43} \right) + 150\);
c) \(\left( { - 15} \right).40:6\);
d) \(125.\left( { - 7} \right) + 14.\left( { - 125} \right) + 125\).
Thực hiện phép tính (tính hợp lí nếu có thể):
a) \(160 - \left( {{{4.5}^2} - {{3.2}^3}} \right)\);
b) \(43 + \left( { - 100} \right) + \left( { - 43} \right) + 150\);
c) \(\left( { - 15} \right).40:6\);
d) \(125.\left( { - 7} \right) + 14.\left( { - 125} \right) + 125\).
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 6 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
a) \(160 - \left( {{{4.5}^2} - {{3.2}^3}} \right)\)
\( = 160 - \left( {4.25 - 3.8} \right)\)
\( = 160 - \left( {100 - 24} \right)\)
\( = 160 - 100 + 24\)
\( = 60 + 24\)
\( = 84\).
c) \(\left( { - 15} \right).40:6\)
\( = \left( { - 600} \right):6\)
\( = - 100\).b) \(43 + \left( { - 100} \right) + \left( { - 43} \right) + 150\)
\[ = \left[ {43 + \left( { - 43} \right)} \right] + \left[ {\left( { - 100} \right) + 150} \right]\]
\( = 0 + 50\)
\( = 50\).
d) \(125.\left( { - 7} \right) + 14.\left( { - 125} \right) + 125\)
\( = 125.\left( { - 7} \right) - 125.14 + 125.1\)
\( = 125.\left( { - 7 - 14 + 1} \right)\)
\( = 125.\left( { - 20} \right)\)
\( = - 2500\).Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Gọi cạnh hình vuông lớn nhất là \(x\) \[\left( {{\rm{cm}}} \right)\]\(\left( {0 < x < 90} \right)\).
Để cắt tờ bìa hình chữ nhật thành những hình vuông bằng nhau thì \(120 \vdots x\) và \(90 \vdots x\).
Do đó \(x = \)ƯCLN\(\left( {120,90} \right)\)
Ta có: \(120 = {2^3}.3.5\) và \[90 = {2.3^2}.5\].
Suy ra \(x = \)ƯCLN\(\left( {120,90} \right) = 2.3.5 = 30\)
Vậy cạnh hình vuông lớn nhất là \(30\,\,{\rm{cm}}\).
Diện tích của tờ bìa hình chữ nhật ban đầu là: \(120.90 = 10\,\,800\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\).
Diện tích tờ bìa mỗi hình vuông cắt được là: \[30.30 = 900\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right)\].
Số tờ bìa hình vuông cắt được là: \(10\,\,800:900 = 12\) (tờ).
Lời giải
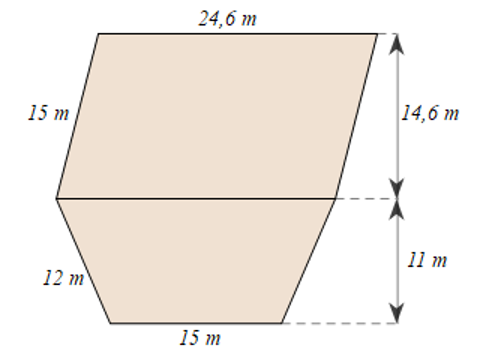
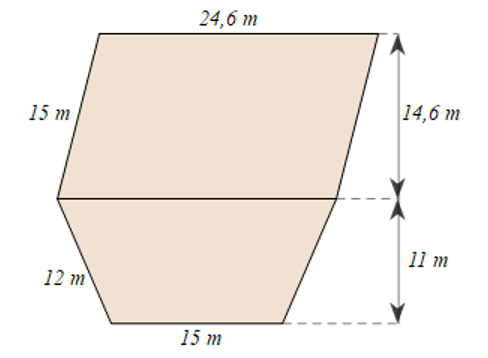
a) Diện tích phần ruộng hình bình hành là:
\(14,6.24,6 = 359,16\left( {{m^2}} \right)\)
Diện tích phần ruộng hình thang cân là:
\(\frac{{\left( {24,6 + 15} \right).11}}{2} = 217,8\left( {{m^2}} \right)\)
Diện tích thửa ruộng là:
\(359,16 + 217,8 = 576,96\left( {{m^2}} \right)\).
b) Mỗi vụ bác Lan thu hoạch được số kilôgam thóc là:
\(576,96.0,7 = 403,872\left( {kg} \right)\).
Câu 3
A. Hoa lưu ly chỉ có tâm đối xứng;
B. Hoa lưu ly chỉ có trục đối xứng;
C. Hoa lưu ly có trục đối xứng và có tâm đối xứng;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
A. Hình tam giác đều, hình vuông;
B. Hình vuông, hình tam giác đều, hình lục giác đều;
C. Hình vuông, hình thoi, hình lục giác đều, hình chữ nhật;
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.