Một hộp giấy đựng bỏng ngô gồm bốn mặt bên xung quanh và một mặt đáy. Biết mỗi mặt xung quanh của một hộp giấy đó có dạng là một hình thang cân có độ dài các cạnh đáy lần lượt là \(13cm\) và \(10cm\), chiều cao là \(20cm\); đáy hộp có dạng hình vuông cạnh là \(10cm\).

a) Tính diện tích một mặt bên của hộp giấy.
b) Hỏi cần ít nhất bao nhiêu cen-ti-mét vuông giấy bìa để làm một chiếc hộp đựng bỏng ngô đó? (không tính diện tích các mép dán)
Một hộp giấy đựng bỏng ngô gồm bốn mặt bên xung quanh và một mặt đáy. Biết mỗi mặt xung quanh của một hộp giấy đó có dạng là một hình thang cân có độ dài các cạnh đáy lần lượt là \(13cm\) và \(10cm\), chiều cao là \(20cm\); đáy hộp có dạng hình vuông cạnh là \(10cm\).

a) Tính diện tích một mặt bên của hộp giấy.
b) Hỏi cần ít nhất bao nhiêu cen-ti-mét vuông giấy bìa để làm một chiếc hộp đựng bỏng ngô đó? (không tính diện tích các mép dán)
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 6 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
a) Diện tích một mặt của hộp giấy là:
\(\frac{{\left( {10 + 13} \right).20}}{2} = 230\,\,\left( {c{m^2}} \right)\)
b) Diện tích bốn mặt xung quanh của chiếc hộp là:
\(230.\,4\,\, = \,\,920\,\left( {c{m^2}} \right)\)
Đáy hộp đựng bỏng ngô là hình vuông nên có diện tích là:
\(10.\,10 = \,100\,\,\left( {c{m^2}} \right)\)
Diện tích giấy bìa ít nhất để làm được một chiếc hộp là:
\(920\, + \,100\,\, = \,\,1020\,\left( {c{m^2}} \right)\).
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
Với mọi số nguyên \(n\) ta có:
\(3n - 1 = 3n - 6 + 5 = 3\left( {n - 2} \right) + 5\)
Vì \(\left( {3n - 1} \right) \vdots \left( {n - 2} \right)\) nên \(\left[ {3\left( {n - 2} \right) + 5} \right] \vdots \left( {n - 2} \right)\)
Mà \(3\left( {n - 2} \right) \vdots \left( {n - 2} \right)\), suy ra \(5 \vdots \left( {n - 2} \right)\)
Do đó \(\left( {n - 2} \right) \in \)Ư(5) \( = \left\{ { - 5; - 1;1;5} \right\}\)
Ta có bảng sau:
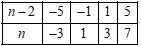
Đối chiếu điều kiện \(n\) là số nguyên ta thấy các giá trị \(n\) tìm được ở trên đều thỏa mãn.
Vậy \(n \in \left\{ { - 3;1;3;7} \right\}\).
Lời giải
Do 32 học sinh lớp 6A, 48 học sinh lớp 6B, 56 học sinh lớp 6C xếp thành các hàng dọc bằng nhau nên số hàng dọc nhiều nhất có thể xếp được là ước chung lớn nhất của 32, 48 và 56.
Ta có: \(32 = {2^5};\,\,\,\,48 = {2^4}.3;\,\,\,\,56 = {2^3}.7\)
ƯCLN\(\left( {32,48,56} \right) = {2^3} = 8\).
Vậy mỗi lớp xếp được nhiều nhất 8 hàng dọc.
Khi đó lớp 6A có \(32:8 = 4\) hàng ngang;
lớp 6B có \[48:8 = 6\] hàng ngang;
lớp 6C có \[56:8 = 7\] hàng ngang.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 4
A. \(A = \left\{ {36} \right\}\);
B. \(A = \left\{ {36;48} \right\}\);
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 5
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Câu 6
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.