Cho biết năm sinh của một số nhà toán học:
Tên nhà Toán học
Năm sinh
Archimedes
287 TCN
Pythagore
570 TCN
Descartes
1596
Lương Thế Vinh
1441
Sắp xếp các nhà Toán học theo thứ tự giảm dần của năm sinh ta được:
Cho biết năm sinh của một số nhà toán học:
|
Tên nhà Toán học |
Năm sinh |
|
Archimedes |
287 TCN |
|
Pythagore |
570 TCN |
|
Descartes |
1596 |
|
Lương Thế Vinh |
1441 |
Sắp xếp các nhà Toán học theo thứ tự giảm dần của năm sinh ta được:
A. Descartes, Lương Thế Vinh, Archimedes, Pythagore;
B. Descartes, Lương Thế Vinh, Pythagore, Archimedes;
C. Archimedes, Pythagore, Lương Thế Vinh, Descartes;
Câu hỏi trong đề: Bộ 10 đề thi cuối kì 1 Toán 6 Cánh diều có đáp án !!
Quảng cáo
Trả lời:
Đáp án đúng là: A
Ta có bảng sau:
|
Tên nhà Toán học |
Năm sinh |
|
Archimedes |
–287 |
|
Pythagore |
–570 |
|
Descartes |
1596 |
|
Lương Thế Vinh |
1441 |
Ta có: \(1596 > 1441 > - 287 > - 570\).
Sắp xếp các nhà Toán học theo thứ tự giảm dần của năm sinh ta được: Descartes, Lương Thế Vinh, Archimedes, Pythagore.
Hot: 1000+ Đề thi giữa kì 2 file word cấu trúc mới 2026 Toán, Văn, Anh... lớp 1-12 (chỉ từ 60k). Tải ngay
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Lời giải
a) Chiều dài của hình nền nhà hình chữ nhật đó là: 5 + 3 = 8 (m)
Diện tích nền phòng học đó là: \[5.8 = 40\,\,\left( {{{\rm{m}}^2}} \right)\].
b) Diện tích một viên gạch men hình vuông cạnh \(40\,\,{\rm{cm}}\) là:
\(40.40 = 1600\,\,\left( {{\rm{c}}{{\rm{m}}^2}} \right) = 0,16\,\,\left( {{{\rm{m}}^2}} \right)\).
Số viên gạch cần dùng để lát nền căn phòng là:
\(40:0,16 = 250\) (viên).
Do đó cần 250 viên gạch để lát nền phòng học.
Số tiền mua gạch men là:
\(24{\rm{ }}000 . 250= 6{\rm{ 000 }}000\) (đồng).
Số tiền công lát nền là:
\(50{\rm{ }}000 . 40= 2{\rm{ 000 }}000\) (đồng).
Vậy tổng số tiền phải trả để lát nền căn phòng học đó là:
\[6{\rm{ 000 }}000 + 2{\rm{ 000 }}000 = 8{\rm{ }}000{\rm{ }}000\] (đồng).
Lời giải
Ta có: \[xy + 3x + 3y = --16\]
\(\left( {xy + 3x} \right) + \left( {3y + 9} \right) = - 16 + 9\)
\[x\left( {y + 3} \right) + 3\left( {y + 3} \right) = - 7\]
\[\left( {y + 3} \right)\left( {x + 3} \right) = - 7 = \left( { - 7} \right).1 = 1.\left( { - 7} \right) = 7.\left( { - 1} \right) = \left( { - 1} \right).7\]
Với \(x,y\) là các số nguyên thì \(x + 3\) và \(y + 3\) cũng là số nguyên, do đó ta có bảng sau:
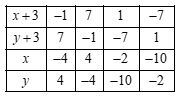
Vậy \(\left( {x;y} \right) \in \left\{ {\left( { - 4;4} \right);\left( {4; - 4} \right);\left( { - 2; - 10} \right);\left( { - 10; - 2} \right)} \right\}\).
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.
Lời giải
Bạn cần đăng ký gói VIP ( giá chỉ từ 199K ) để làm bài, xem đáp án và lời giải chi tiết không giới hạn.